
Vzorec F-testu (obsah)
- vzorec
- Príklady
Čo je vzorec F-testu?
F-test je štatistický test, ktorý nám pomáha pri zisťovaní, či dve skupiny populácií, ktoré majú normálne rozloženie svojich dátových bodov, majú rovnakú štandardnú odchýlku alebo odchýlku. Prvá a najdôležitejšia vec na vykonanie F-testu je však to, že súbory údajov by mali mať normálnu distribúciu. Toto sa aplikuje na distribúciu F pod nulovou hypotézou. F-test je veľmi dôležitou súčasťou analýzy variácie (ANOVA) a vypočíta sa pomocou pomerov dvoch variantov dvoch rôznych súborov údajov. Ako vieme, tieto odchýlky nám poskytujú informácie o rozptyle údajových bodov. F-test sa používa aj pri rôznych testoch, ako je regresná analýza, Chowov test atď.
Vzorec pre F-test:
Neexistuje jednoduchý vzorec pre F-Test, ale je to rad krokov, ktoré musíme nasledovať:
Krok 1: Na vykonanie F-testu musíme najskôr definovať nulovú hypotézu a alternatívnu hypotézu. Sú uvedené: -
- H0 (nulová hypotéza): Variácia 1. súboru údajov = Variant 2. súboru údajov
- Ha: Odchýlka 1. súboru údajov <Odchýlka 2. súboru údajov (pre dolný jednostranný test)
- Ha: Odchýlka 1. súboru údajov> Odchýlka 2. súboru údajov (pre hornú jednostrannú skúšku)
- Ha: Odchýlka od 1. súboru údajov ≠ Odchýlka od druhého súboru údajov (pre dvojstranný test)
Krok 2: Ďalšou vecou, ktorú musíme urobiť, je, že musíme zistiť úroveň významnosti a potom určiť stupne slobody čitateľa aj menovateľa. To nám pomáha pri určovaní ich kritických hodnôt. Stupeň voľnosti je veľkosť vzorky -1.
Krok 3: F-testovací vzorec:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Krok 4: Nájdite kritickú hodnotu F z tabuľky F s mierou voľnosti a úrovne významnosti.
Krok 5: Porovnajte tieto dve hodnoty a ak je kritická hodnota menšia ako hodnota F, môžete zamietnuť nulovú hypotézu.
Príklady vzorcov F-testu (so šablónou programu Excel)
Vezmime príklad, aby sme lepšie pochopili výpočet F-testu.
Túto šablónu vzorcov Excel F-TEST si môžete stiahnuť tu - šablónu vzorcov Excel F-TESTVzorec F-testu - príklad č
Povedzme, že máme dve sady údajov A a B, ktoré obsahujú rôzne údajové body. Vykonajte F-test, aby ste zistili, či môžeme zamietnuť nulovú hypotézu na hladine významnosti 1%.
Množiny údajov:
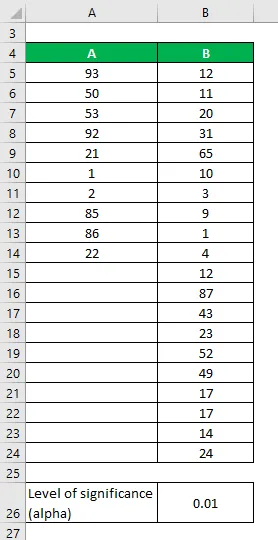
Riešenie:
Nulová hypotéza: Variant A = Variant B
Stupeň slobody sa vypočíta ako
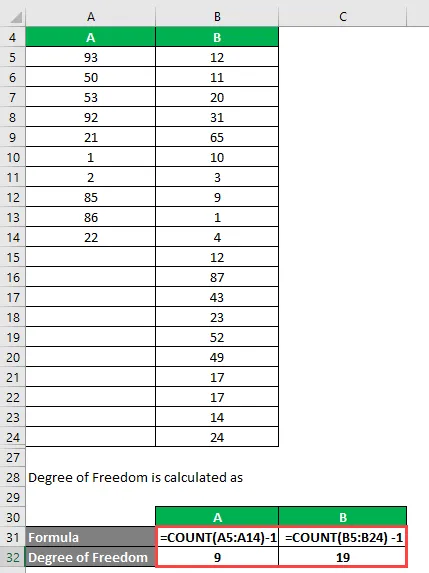
Stupeň slobody
- Pre A = 10 - 1 = 9
- Pre B = 20 - 1 = 19
Variácia sa vypočíta ako:

- Varianta A = 1385, 61
- Varianta B = 521, 22
F Hodnota sa vypočíta pomocou vzorca uvedeného nižšie
F Hodnota = variácia 1. súboru údajov / variácia 2. súboru údajov
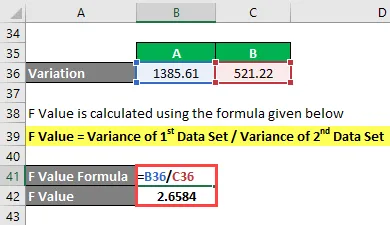
- F Hodnota = 1385, 61 / 521, 22
- F hodnota = 2, 6584
F-tabuľka:
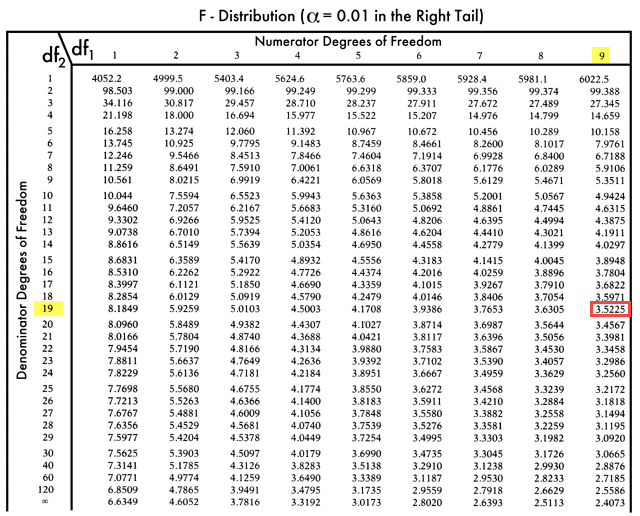
Kritická hodnota F = 3, 5225
Pretože hodnota F critical je vyššia ako hodnota F, nemôžeme odmietnuť nulovú hypotézu.
Vzorec F-testu - príklad č. 2
Predpokladajme, že pracujete vo výskumnej spoločnosti a chcete, aby úroveň emisií oxidu uhličitého, ku ktorej dochádza u 2 rôznych značiek cigariet, a či sú výrazne odlišné alebo nie. Vo svojej analýze ste zhromaždili nasledujúce informácie:
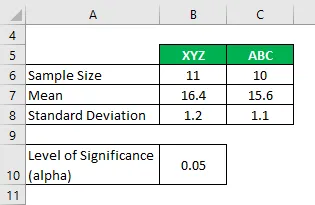
Riešenie:
Stupeň slobody sa vypočíta ako
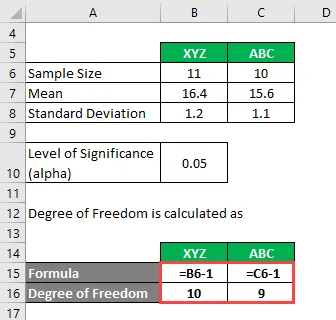
Stupeň slobody
- Pre XYZ = 11 - 1 = 10
- Pre ABC = 10 - 1 = 9
Variácia sa vypočíta ako:
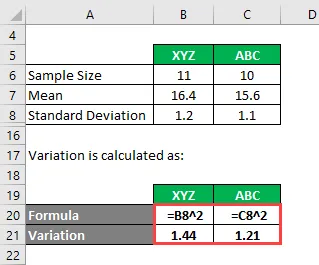
- Variácia XYZ = 1, 2 2 = 1, 44
- Varianta ABC = 1, 1 2 = 1, 21
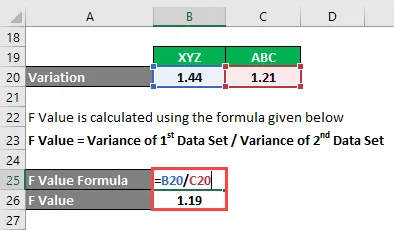
- F hodnota = 1, 44 / 1, 21
- F hodnota = 1, 19
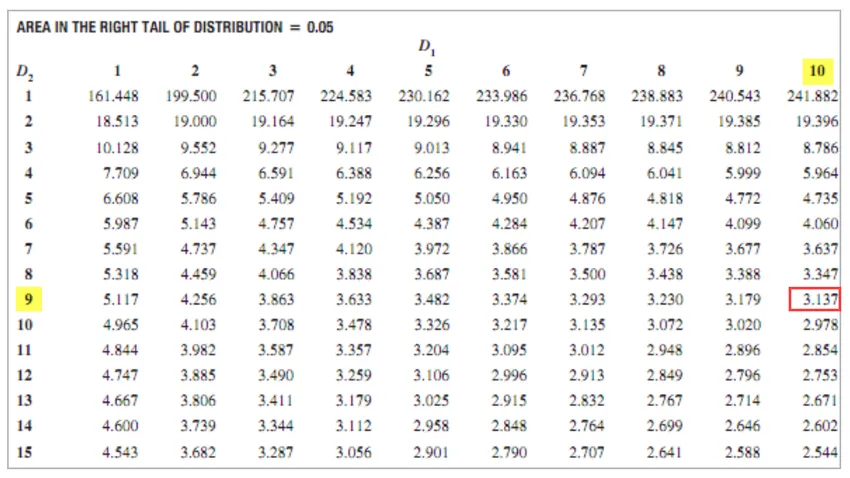
F Kritická hodnota = 3, 137
Pretože hodnota F kritická> F nie je možné zamietnuť nulovú hypotézu.
vysvetlenie
Vo vyššie uvedených príkladoch sme videli použitie F-testu a ako sa vykonáva. Ale existuje súbor predpokladov, ktoré musíme pred vykonaním F-testu postarať, inak nedostaneme požadované výsledky:
- Prvá vec je, že pri výpočte hodnoty F musíme vždy umiestniť čitateľ s vyššou odchýlkou hodnoty. Takže ak F = V1 / V2, V1 by malo byť> V2
- Ak chceme vykonať 2 chvostové testy, musíme deliť hladinu významnosti 2 a to bude správna úroveň na nájdenie kritickej hodnoty.
- Rozptyl používame iba na výpočet hodnoty F a ak sa dostaneme so štandardnými odchýlkami, ako v príklade 2, na nájdenie rozptylu sa musia zaokrúhliť na druhú.
- Vzorky by mali byť navzájom nezávislé a veľkosť vzorky by mala byť menšia ako 30
- Súbory populácií, z ktorých sa vzorky odoberajú, sa musia normálne distribuovať
Toto sú kľúčové parametre / predpoklad, o ktoré by ste sa mali pri vykonávaní testu F postarať.
Relevantnosť a použitie F-testovacieho vzorca
F-Test, ako je uvedené vyššie, nám pomáha kontrolovať rovnosť dvoch rozdielov v populácii. Takže, keď máme dve nezávislé vzorky, ktoré boli vybrané z normálnej populácie a chceme skontrolovať, či majú rovnakú variabilitu, použijeme F-test. F-test má tiež veľký význam v regresnej analýze a tiež na testovanie významnosti R2. Stručne povedané, F-test je veľmi dôležitým nástrojom v štatistike, ak chceme porovnať variácie 2 alebo viacerých súborov údajov. Pred vykonaním tohto testu by ste však mali mať na pamäti všetky predpoklady.
Odporúčané články
Toto bol sprievodca F-testovou formuláciou. Tu diskutujeme o výpočte F-testu spolu s praktickými príkladmi a stiahnuteľnou šablónou Excel. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- T Distribučný vzorec
- Vzorec pre stanovenie ceny dlhopisov
- Vzorec percentuálnej chyby
- Výpočet vzorca NOPAT