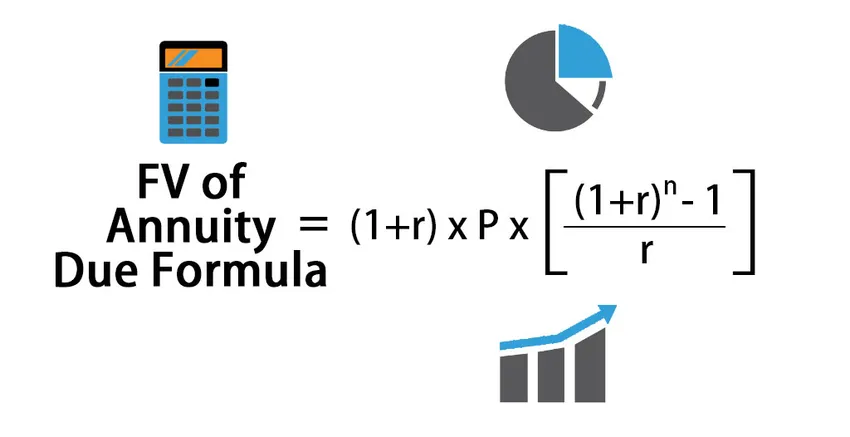
Budúca hodnota splatného dôchodku (obsah)
- Budúca hodnota splatného dôchodku
- Príklady budúcej hodnoty splatného dôchodku (so šablónou programu Excel)
- Budúca hodnota anuity Due Formula Calculator
Budúca hodnota splatného dôchodku
Vzorec na výpočet budúcej hodnoty splatnej anuity:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Kde,
- P = pravidelná platba
- R = sadzba za obdobie
- N = počet období
Príklady budúcej hodnoty splatného dôchodku (so šablónou programu Excel)
Vezmime príklad, aby sme lepšie pochopili výpočet budúcej hodnoty splatného dôchodku.
Túto budúcu hodnotu vzoru anuitnej splatnosti podľa vzorca Excel si môžete stiahnuť tu - budúcu hodnotu anuitnej splatnosti podľa vzorca ExcelPríklad č. 1
Predpokladajme, že Anand vložil 10 000 dolárov ročne a efektívna miera, ktorú ponúka jeho účet, je 3%. Teraz chce Anand počítať svoj budúci zostatok po 5 rokoch s predpokladom prvého vkladu od dnešného dňa.
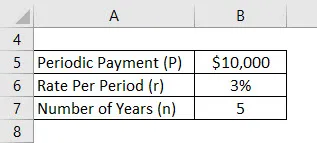
Riešenie:
Budúca hodnota splatnosti anuity sa vypočíta pomocou vzorca uvedeného nižšie
FV splatnosti anuity = (1 + r) * P * (((1 + r) n - 1) / r)
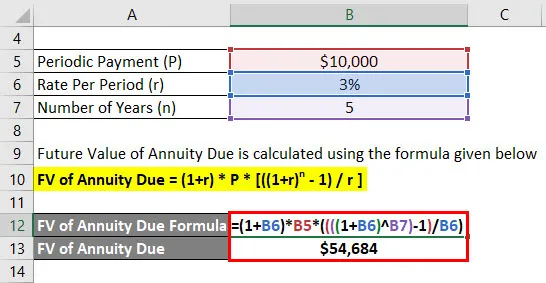
- FV splatnosti anuity = (1+ 3%) * 10 000 $ * (((((1 + 3%) 5) - 1) / 3%))
- FV splatnej anuity = 54 684 dolárov
Po piatich rokoch získa Anand budúci zostatok 54 684 dolárov.
Príklad č. 2
Predpokladajme, že Jagriti vložilo 8 000 dolárov ročne a efektívna miera, ktorú jeho účet ponúka, je 5%. Teraz chce Jagriti počítať svoj budúci zostatok po 5 rokoch s predpokladom prvého vkladu od dnešného dňa.

Riešenie:
Budúca hodnota splatnosti anuity sa vypočíta pomocou vzorca uvedeného nižšie
FV splatnosti anuity = (1 + r) * P * (((1 + r) n - 1) / r)
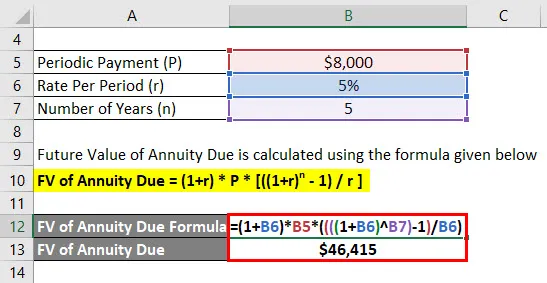
- FV splatnosti anuity = (1+ 5%) * 8 000 $ * (((((1 + 5%) 5) - 1) / 5%)
- FV splatnej anuity = 46 415 dolárov
Jagriti získa budúci zostatok 46 415 dolárov po 5 rokoch.
Príklad č. 3
Predpokladajme, že Anandriti vložil 20 000 dolárov ročne a efektívna miera, ktorú jeho účet ponúka, je 2%. Teraz chce Anandriti počítať svoj budúci zostatok po 5 rokoch s predpokladom prvého vkladu od dnešného dňa.
Riešenie:
Budúca hodnota splatnosti anuity sa vypočíta pomocou vzorca uvedeného nižšie
FV splatnosti anuity = (1 + r) * P * (((1 + r) n - 1) / r)
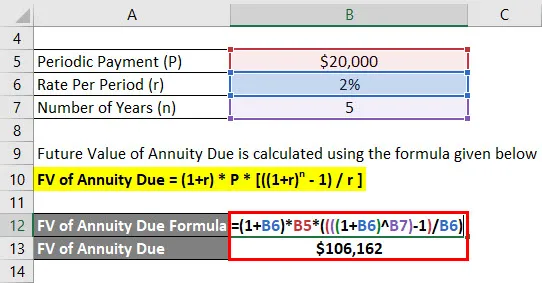
- FV splatnosti anuity = (1+ 2%) * 20 000 $ * (((((1 + 2%) 5) - 1) / 2%))
- FV splatnej anuity = 1 066 162 USD
Anandriti získa budúci zostatok vo výške 1 06 162 dolárov po 5 rokoch.
vysvetlenie
Na výpočet konečnej hodnoty pre rad peňažných tokov alebo platieb, pri ktorých je prvá splátka prijatá okamžite, použijeme budúcu hodnotu splatnej anuity. Prvá okamžitá splátka alebo platba rozlišuje rentu z dôvodu riadnej renty. Okamžitá alebo okamžitá anuita sa označuje ako splatná anuita.
Vypočítava hodnotu peňažných tokov v budúcom období. Použitie FV splatnej anuity je v skutočných situáciách odlišné od súčasnej hodnoty splatnej anuity. Predpokladajme napríklad, že spoločnosť alebo jednotlivec kupuje anuitu a zaplatil prvú splátku dnes. Pomocou tohto príkladu môžeme ďalej vysvetliť, predpokladať, že spoločnosť alebo jednotlivec chce od kohokoľvek kúpiť anuitu a dnes uskutočnil prvú platbu. Na výpočet ceny, ktorá sa má zaplatiť v tejto situácii, môžeme použiť súčasnú hodnotu vzorca pre výpočet anuity. Ak však chceme zostatok zostatku vypočítať po uložení úroku po dobu 5 rokov na účte a dnes sme sa rozhodli vyplatiť prvú splátku, v tomto prípade sa použije budúca hodnota anuity. Splatnosť anuity sa dá vysvetliť ako druh anuity, keď sa peňažné toky vyskytujú na začiatku každého obdobia. Vzhľadom na pokročilý charakter peňažných tokov podlieha každý peňažný tok zloženému efektu za každé ďalšie obdobie v prípade, že sa porovnáva s bežnou anuitou. Budúca hodnota bežnej anuity je nižšia ako budúca hodnota anuity, pretože budúca hodnota anuity dostáva periodický úrok faktoru jedna plus.
Relevantnosť a použitie budúcej hodnoty splatného dôchodku
Pochopme význam budúcej hodnoty a renty splatnej osobitne. Budúca hodnota sa dá vysvetliť ako celková hodnota sumy hotovosti, ktorá sa má zaplatiť v budúcnosti k určitému dátumu. Splatná anuita sa dá vysvetliť ako séria platieb, ktoré sa uskutočňujú na začiatku každého obdobia v pravidelnom poradí. Budúca hodnota splatnej anuity sa preto dá vysvetliť ako celková hodnota k určitému budúcemu dátumu pre sériu systematických / pravidelných platieb, ak sa platby uskutočňujú na začiatku každého obdobia. Tento typ transakcie a taký tok platieb je možné vidieť na účte príjemcu dôchodkového plánu. Celková hodnota je suma, do ktorej sa séria platieb uskutočnených v budúcom dátume vzrastie, keď sa predpokladá určitá výška úroku, a príjmy sa v priebehu určitého obdobia postupne zvyšujú. Výpočet budúcej hodnoty bežnej renty je totožný s týmto, ale jediným rozdielom je, že pripočítame dodatočnú lehotu splatnosti, ktorá sa vykonáva na začiatku.
Budúca hodnota anuity Due Formula Calculator
Môžete použiť nasledujúcu kalkulačku budúcej hodnoty anuity
| P | |
| r | |
| n | |
| Budúca hodnota splatného dôchodku | |
| Budúca hodnota splatného dôchodku | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Odporúčané články
Toto bol návod na výpočet budúcej hodnoty povinného dôchodku. Tu diskutujeme o tom, ako vypočítať budúcu hodnotu povinného dôchodku spolu s praktickými príkladmi. Poskytujeme tiež kalkulačku budúcej hodnoty anuity Due s možnosťou stiahnutia z Excel šablóny. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Sprievodca časovou hodnotou peňazí
- Príklady vzorca súčasnej hodnoty
- Kalkulačka pre výpočet pomeru informácií
- Vzorec pre stupeň prevádzkového pákového efektu