Rozdiel medzi lineárnou regresiou a logistickou regresiou
Nasledujúci článok Lineárna regresia verzus logistická regresia poskytuje najdôležitejšie rozdiely medzi oboma, ale skôr ako uvidíme, čo znamená regresia?
regresia
Regresia je v podstate štatistické opatrenie na stanovenie sily vzťahu medzi jednou závislou premennou, tj výstupom Y a radom ďalších nezávislých premenných, tj X 1, X 2 atď. Regresná analýza sa v zásade používa na predpovedanie a predpovedanie.
Čo je lineárna regresia?
Lineárna regresia je algoritmus, ktorý je založený na kontrolovanej oblasti učenia strojového učenia. Zdedí lineárny vzťah medzi svojimi vstupnými premennými a jednoduchou výstupnou premennou, ak je výstupná premenná svojou povahou súvislá. Používa sa na predpovedanie hodnoty výstupu, povedzme Y zo vstupov, povedzme X. Keď sa uvažuje iba o jednom vstupe, nazýva sa to jednoduchá lineárna regresia.
Dá sa rozdeliť do dvoch hlavných kategórií:
1. Jednoduchá regresia
Princíp činnosti: Hlavným cieľom je zistiť rovnicu priamky, ktorá najlepšie vyhovuje vzorkovaným údajom. Táto rovnica algebraicky popisuje vzťah medzi týmito dvoma premennými. Najpriaznivejšia priamka sa nazýva regresná priamka.
Y = β 0 + β 1 X
Kde,
p predstavuje znaky
p 0 predstavuje priesečník
pi predstavuje koeficient funkcie X
2. Multivariabilná regresia
Používa sa na predpovedanie korelácie medzi viac ako jednou nezávislou premennou a jednou závislou premennou. Regresia s viac ako dvoma nezávislými premennými je založená na tvarovom usporiadaní konštelácie dát na viacrozmernom grafe. Tvar regresie by mal byť taký, aby minimalizoval vzdialenosť tvaru od každého údajového bodu.
Lineárny vzťahový model možno matematicky znázorniť takto:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Kde,
p predstavuje znaky
p 0 predstavuje priesečník
pi predstavuje koeficient funkcie X1
p predstavuje koeficient funkcie Xn
Výhody a nevýhody lineárnej regresie
Nižšie sú uvedené výhody a nevýhody:
výhody
- Kvôli svojej jednoduchosti sa bežne používa na modelovanie predpovedí a inferencií.
- Zameriava sa na analýzu údajov a ich spracovanie. Zaoberá sa teda rôznymi údajmi bez toho, aby sa obťažovali detailami o modeli.
nevýhody
- Funguje efektívne, keď sú dáta bežne distribuované. Preto pre efektívne modelovanie je potrebné sa vyhnúť kolinearite.
Čo je to logistická regresia?
Je to forma regresie, ktorá umožňuje predikciu diskrétnych premenných pomocou zmesi spojitých a diskrétnych prediktorov. Výsledkom je jedinečná transformácia závislých premenných, ktorá ovplyvňuje nielen proces odhadovania, ale aj koeficienty nezávislých premenných. Zaoberá sa rovnakou otázkou, ktorú robí viacnásobná regresia, ale bez distribučných predpokladov na prediktoroch. V logistickej regresii je výsledná premenná binárna. Účelom analýzy je posúdiť účinky viacerých vysvetľujúcich premenných, ktoré môžu byť číselné alebo kategorické alebo obidve.
Druhy logistickej regresie
Nižšie sú uvedené dva typy logistickej regresie:
1. Binárna logistická regresia
Používa sa, keď závislá premenná je dichotomická, tj ako strom s dvoma vetvami. Používa sa, keď závislá premenná nie je parametrická.
Používa sa, keď
- Ak neexistuje linearita
- Existujú iba dve úrovne závislej premennej.
- Ak je pochybnosť o viacrozmernej normálnosti.
2. Multinomická logistická regresia
Multinomická logistická regresná analýza vyžaduje, aby boli nezávislé premenné metrické alebo dichotomické. Neuvádza žiadne predpoklady linearity, normality a homogenity rozptylu pre nezávislé premenné.
Používa sa, keď závislá premenná má viac ako dve kategórie. Používa sa na analýzu vzťahov medzi nemetrickými závislými premennými a metrickými alebo dichotomickými nezávislými premennými, potom porovnáva viaceré skupiny kombináciou binárnych logistických regresií. Nakoniec poskytuje súbor koeficientov pre každé z týchto dvoch porovnaní. Koeficienty pre referenčnú skupinu sa považujú za všetky nuly. Nakoniec sa predpovedá na základe najvyššej pravdepodobnosti.
Výhoda logistickej regresie: Je to veľmi účinná a široko používaná technika, pretože nevyžaduje veľa výpočtových zdrojov a nevyžaduje žiadne ladenie.
Nevýhoda logistickej regresie: Nemožno ju použiť na riešenie nelineárnych problémov.
Porovnanie medzi hlavami medzi lineárnou regresiou a logistickou regresiou (infografika)
Nižšie je uvedených šesť najlepších rozdielov medzi lineárnou regresiou a logistickou regresiou 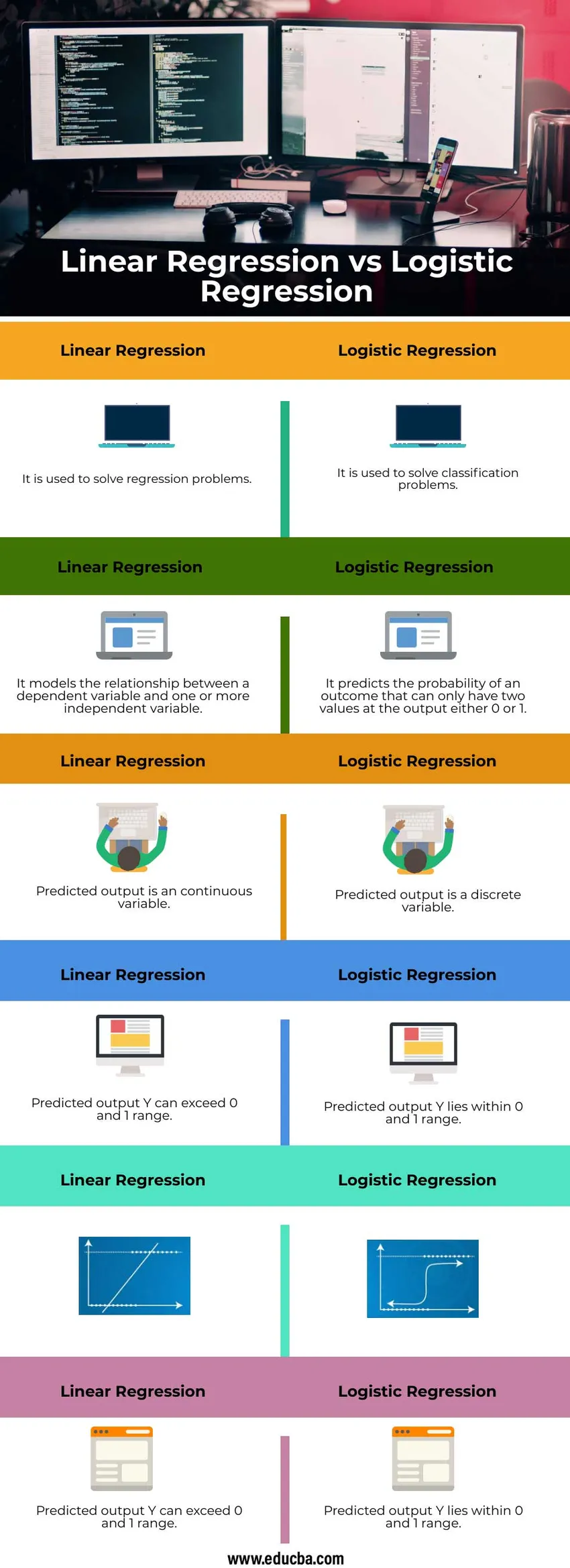
Kľúčový rozdiel medzi lineárnou regresiou a logistickou regresiou
Poďme diskutovať o niektorých hlavných kľúčových rozdieloch medzi lineárnou regresiou a logistickou regresiou
Lineárna regresia
- Je to lineárny prístup
- Používa priamu čiaru
- Nemôže brať kategorické premenné
- Musí ignorovať pozorovania s chýbajúcimi hodnotami numerickej nezávislej premennej
- Výstup Y je uvedený ako
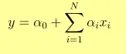
- 1 jednotka nárast x zvyšuje Y o α
aplikácia
- Predpovedanie ceny produktu
- Predpovedanie skóre v zápase
Logistická regresia
- Je to štatistický prístup
- Používa sigmoidnú funkciu
- Môže mať kategorické premenné
- Môže prijímať rozhodnutia, aj keď sú prítomné pripomienky s chýbajúcimi hodnotami
- Výstup Y je uvedený ako, kde z je uvedený ako
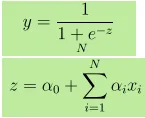
- 1 jednotka zvýšenie x zvyšuje Y logaritmickou pravdepodobnosťou α
- Ak P je pravdepodobnosť udalosti, potom (1-P) je pravdepodobnosť, že sa nevyskytne. Kurzy úspechu = P / 1-P
aplikácia
- Predpovedanie, či dnes prší alebo nie.
- Predpovedanie, či je e-mail spam alebo nie.
Porovnávacia tabuľka lineárnej regresie verzus logistická regresia
Poďme diskutovať o najlepšom porovnaní medzi lineárnou regresiou a logistickou regresiou
|
Lineárna regresia |
Logistická regresia |
| Používa sa na riešenie regresných problémov | Používa sa na riešenie problémov klasifikácie |
| Modeluje vzťah medzi závislou premennou a jednou alebo viacerými nezávislými premennými | Predpovedá pravdepodobnosť výsledku, ktorý môže mať na výstupe iba dve hodnoty buď 0 alebo 1 |
| Predpovedaný výstup je spojitá premenná | Predpovedaný výstup je diskrétna premenná |
| Predpovedaný výkon Y môže prekročiť rozsah 0 a 1 | Predpovedaný výkon Y leží v rozsahu 0 a 1 |
 | 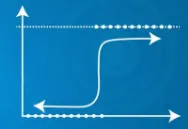 |
| Predpovedaný výkon Y môže prekročiť rozsah 0 a 1 | Predpokladaná produkcia |
záver
Ak funkcie neprispievajú k predikcii alebo ak sú navzájom veľmi korelované, modelu sa pridá šum. Z tohto dôvodu je potrebné odstrániť prvky, ktoré do modelu dostatočne neprispievajú. Ak sú nezávislé premenné vysoko korelované, môže to spôsobiť problém mnohostrannosti, ktorý možno vyriešiť spustením samostatných modelov s každou nezávislou premennou.
Odporúčané články
Toto bol sprievodca lineárnou regresiou vs. logistickou regresiou. Tu diskutujeme kľúčové rozdiely medzi lineárnou regresiou a logistickou regresiou s infografikou a porovnávaciu tabuľku. Ak sa chcete dozvedieť viac, môžete si pozrieť aj nasledujúce články -
- Data Science vs Vizualizácia dát
- Strojové učenie vs neurónová sieť
- Dozorované učenie vs hlboké učenie
- Logistická regresia v R