✅ GLM v R - GLM funkcie a ako vytvoriť GLM v R?

Čo je GLM v R?

Čo je GLM v R?

Generalizované lineárne modely sú podmnožinou lineárnych regresných modelov a účinne podporujú neštandardné distribúcie. Na podporu toho sa odporúča používať funkciu glm (). GLM funguje dobre s premennou, ak rozptyl nie je konštantný a normálne distribuovaný. Funkcia spojenia je definovaná na transformáciu premennej odozvy tak, aby zodpovedala príslušnému modelu. Model LM sa vyrába s rodinou aj so vzorcom. Model GLM má tri kľúčové komponenty, ktoré sa nazývajú náhodné (pravdepodobnosť), systematické (lineárny prediktor), komponent spojenia (pre logitovú funkciu). Výhodou použitia glm je, že majú flexibilitu modelu, nie je potrebné neustále rozptyl a tento model vyhovuje odhadu maximálnej pravdepodobnosti a jeho pomerom. V tejto téme sa dozvieme o GLM v R.

Funkcia GLM

Syntax: glm (vzorec, rodina, údaje, hmotnosti, podmnožina, Start = null, model = TRUE, method = ””…)

Typy rodiny (vrátane typov modelov) zahŕňajú binomické, Poissonove, gaussovské, gama, kvázi. Každá distribúcia vykonáva iné použitie a môže byť použitá v klasifikácii aj predikcii. A keď je model gaussovský, odpoveďou by malo byť skutočné celé číslo.

A keď je model binomický, odpoveďou by mali byť triedy s binárnymi hodnotami.

A keď je modelom Poisson, odpoveď by nemala byť negatívna s číselnou hodnotou.

A keď je modelom gama, odpoveď by mala byť kladná číselná hodnota.

glm.fit () - Prispôsobenie modelu

Lrfit () - označuje logickú regresnú fit.

update () - pomáha pri aktualizácii modelu.

anova () - je to voliteľný test.

Ako vytvoriť GLM v R?

Tu uvidíme, ako vytvoriť ľahký zovšeobecnený lineárny model s binárnymi údajmi pomocou funkcie glm (). A pokračovaním so súborom údajov Stromy.

Príklady

// Importovanie knižnice
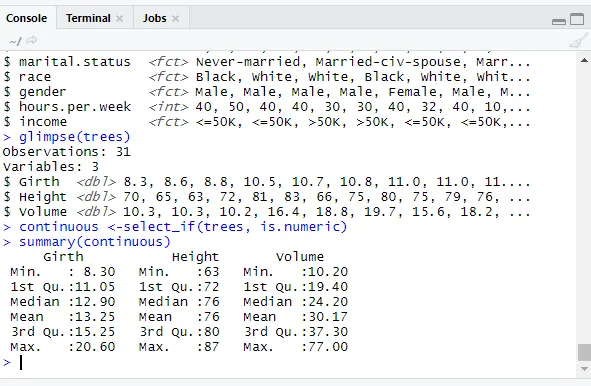
library(dplyr) glimpse(trees)

Na zobrazenie kategorických hodnôt sú priradené faktory.

levels(factor(trees$Girth))

// Overovanie nepretržitých premenných

library(dplyr) continuous <-select_if(trees, is.numeric) summary(continuous)

// Zahrnutie súboru údajov o stromu do prehľadávača R Pathattach (stromy)

x<-glm(Volume~Height+Girth) x

Výkon:

Volajte: glm (vzorec = objem ~ výška + obvod)

koeficienty:

(Priesečník) Výška obvodov

-57, 9877 0, 3393 4, 7082

Stupne slobody: 30 Celkom (tj Null); 28 Zvyšok

Null Deviance: 8106

Zvyšková odchýlka: 421, 9 AIC: 176, 9

summary(x)

volajte:

glm (vzorec = objem ~ výška + obvod)

Zvyšky Deviance:

Min. 1Q Medián 3Q Max

-6, 4065 -2, 6493 -0, 2876 2, 2003 8, 4847

koeficienty:

Odhad Std. Chyba t hodnota Pr (> | t |)

(Intercept) -57, 9877 8, 6382 -6, 713 2, 75e-07 ***

Výška 0.3393 0.1302 2.607 0.0145 *

Obvod 4, 7082 0, 2664 17, 816 <2e-16 ***

Výrazným spôsobe. kódy: 0 '***' 0, 001 '**' 0, 01 '*' 0, 05 '.' 0, 1 '' 1

(Parameter dispergácie pre gaussovskú rodinu bol 15.06862)

Nulová odchýlka: 8106, 08 pri 30 stupňoch voľnosti

Zvyšková odchýlka: 421, 92 pri 28 stupňoch voľnosti

AIC: 176, 91

Počet iterácií podľa Fishera: 2

Výstup sumarizovanej funkcie poskytuje hovory, koeficienty a zvyšky. Vyššie uvedená odozva ukazuje, že koefektívna výška aj obvodový obvod nie sú významné, pretože ich pravdepodobnosť je menšia ako 0, 5. A existujú dva varianty odchýlky nazvané nulová a zvyšková. A konečne, hodnotenie rybárov je algoritmus, ktorý rieši problémy s najväčšou pravdepodobnosťou. V prípade binomie je odpoveďou vektor alebo matica. cbind () sa používa na naviazanie vektorov stĺpca v matici. A na získanie podrobných informácií o súhrne zhody sa používa.

Ak chcete urobiť ako test kapoty, spustí sa nasledujúci kód.

step(x, test="LRT") Start: AIC=176.91 Volume ~ Height + Girth Df Deviance AIC scaled dev. Pr(>Chi) 421.9 176.91 - Height 1 524.3 181.65 6.735 0.009455 ** - Girth 1 5204.9 252.80 77.889 < 2.2e-16 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Call: glm(formula = Volume ~ Height + Girth) Coefficients: (Intercept) Height Girth -57.9877 0.3393 4.7082 Degrees of Freedom: 30 Total (ie Null); 28 Residual Null Deviance: 8106 Residual Deviance: 421.9 AIC: 176.9

Model fit

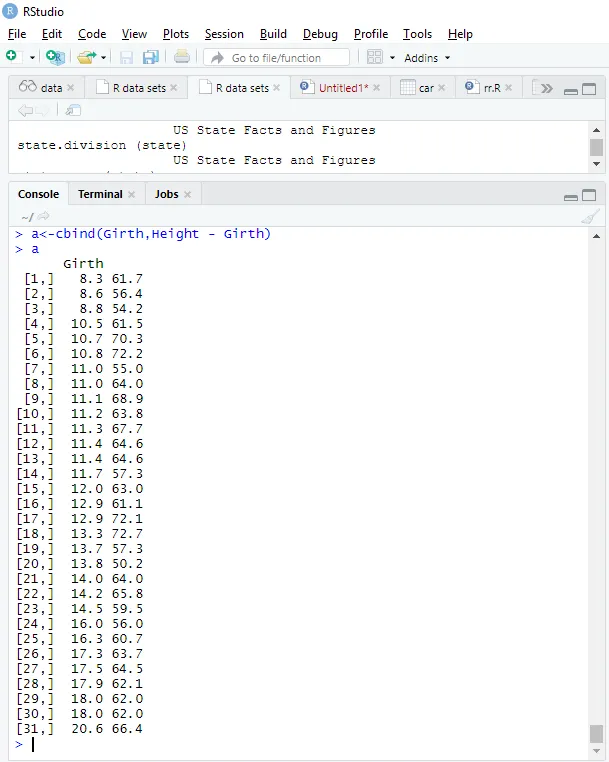
a<-cbind(Height, Girth - Height) > a

zhrnutie (stromy)

Girth Height Volume Min. : 8.30 Min. :63 Min. :10.20 1st Qu.:11.05 1st Qu.:72 1st Qu.:19.40 Median :12.90 Median :76 Median :24.20 Mean :13.25 Mean :76 Mean :30.17 3rd Qu.:15.25 3rd Qu.:80 3rd Qu.:37.30 Max. :20.60 Max. :87 Max. :77.00

Na získanie príslušnej štandardnej odchýlky

apply(trees, sd) Girth Height Volume 3.138139 6.371813 16.437846 predict <- predict(logit, data_test, type = 'response')

Ďalej sa odvolávame na premennú počet odoziev na modelovanie vhodnej odpovede. Na jej výpočet použijeme súbor údajov USAccDeath.

Vstúpte do konzoly R do nasledujúcich úryvkov a zistite, ako sa na nich vykonáva počítanie roku a námestie.

data("USAccDeaths") force(USAccDeaths)

// Analyzovať rok 1973-1978.

disc <- data.frame(count=as.numeric(USAccDeaths), year=seq(0, (length(USAccDeaths)-1), 1))) yearSqr=disc$year^2 a1 <- glm(count~year+yearSqr, family="poisson", data=disc) summary(a1)

volajte:

glm (formula = count ~ year + yearSqr, family = “poisson”, data = disc)

Zvyšky Deviance:

Min. 1Q Medián 3Q Max

-22, 4344 -6, 4401 -0, 0981 6, 0508 21, 4578

koeficienty:

Odhad Std. Chyba z hodnota Pr (> | z |)

(Intercept) 9, 187e + 00 3, 557e-03 2582, 49 <2e-16 ***

rok -7, 207e-03 2, 354e-04 -30, 62 <2e-16 ***

yearSqr 8, 841e-05 3, 221e-06 27, 45 <2e-16 ***

Výrazným spôsobe. kódy: 0 '***' 0, 001 '**' 0, 01 '*' 0, 05 '.' 0, 1 '' 1

(Parameter disperzie pre rodinu Poissonovcov je 1)

Nulová odchýlka: 7357, 4 pri 71 stupňoch voľnosti

Zvyšková odchýlka: 6358, 0 pri 69 stupňoch voľnosti

AIC: 7149, 8

Počet iterácií podľa Fishera: 4

Na overenie najlepšieho prispôsobenia modelu môžete na nájdenie použiť nasledujúci príkaz

zvyšky pre test. Z nižšie uvedeného výsledku je hodnota 0.

1 - pchisq(deviance(a1), df.residual(a1))

(1) 0

Použitie rodiny QuasiPoisson na väčšie rozptyl v daných údajoch

a2 <- glm(count~year+yearSqr, family="quasipoisson", data=disc) summary(a2)

volajte:

glm (formula = count ~ year + yearSqr, family = “quasipoisson”,

data = disk)

Zvyšky Deviance:

Min. 1Q Medián 3Q Max

-22, 4344 -6, 4401 -0, 0981 6, 0508 21, 4578

koeficienty:

Odhad Std. Chyba t hodnota Pr (> | t |)

(Intercept) 9, 187e + 00 3, 417e-02 268, 822 <2e-16 ***

rok -7, 207e-03 2, 261e-03 -3, 188 0, 00216 **

yearSqr 8, 841e-05 3, 095e-05 2, 857 0, 00565 **

(Parameter disperzie pre rodinu kvasipoissonov sa považuje za 92, 2857).

Nulová odchýlka: 7357, 4 pri 71 stupňoch voľnosti

Zvyšková odchýlka: 6358, 0 pri 69 stupňoch voľnosti

AIC: NA

Počet iterácií podľa Fishera: 4

Porovnanie Poissonovej hodnoty s binomickou hodnotou AIC sa výrazne líši. Môžu byť analyzované pomocou presnosti a pomeru spätného volania. Ďalším krokom je overenie, že rozptyl rezíduí je úmerný priemeru. Potom môžeme vykresliť pomocou knižnice ROCR na vylepšenie modelu.

záver

Preto sme sa zamerali na špeciálny model zvaný generalizovaný lineárny model, ktorý pomáha pri zaostrovaní a odhade parametrov modelu. Je to predovšetkým potenciál premennej nepretržitej reakcie. A videli sme, ako glm zapadá do vstavaných balíkov R. Sú to najpopulárnejšie prístupy na meranie počtu údajov a sú to robustné nástroje pre klasifikačné techniky, ktoré využíva vedec údajov. Jazyk R samozrejme pomáha pri zložitých matematických funkciách

Odporúčané články

Toto je príručka pre GLM v R. Tu diskutujeme o funkcii GLM a o tom, ako vytvoriť GLM v R, s príkladmi stromových dát a výstupmi. Viac informácií nájdete aj v nasledujúcom článku -

R Programovací jazyk
Architektúra veľkých dát
Logistická regresia v R
Úlohy na analýzu veľkých dát
Poissonova regresia v R Implementácia Poissonovej regresie

Kategórie:

Veľké dáta

GLM v R - GLM funkcie a ako vytvoriť GLM v R?