
Aritmetický stredný vzorec (obsah)
- vzorec
- Príklady
- kalkulačka
Čo je aritmetický priemerný vzorec?
Termín „aritmetický priemer“ sa v podstate vzťahuje na matematický priemer dvoch alebo viacerých čísel. Metóda výpočtu aritmetického priemeru sa však môže líšiť v závislosti od frekvencie každej premennej v súbore údajov - jednoduchý priemer (rovnako vážený) alebo vážený priemer. Vzorec pre aritmetický priemer pre rovnako vážené premenné možno odvodiť spočítaním všetkých premenných v množine údajov a potom vydelením výsledku počtom premenných. Matematicky je reprezentovaný ako,
Arithmetic Mean = (x 1 + x 2 + …. + x n ) / n
alebo
Arithmetic Mean =∑ x i / n
Kde,
- x i = i. premenná
- n = počet premenných v množine údajov
V prípade nerovnomerne vážených premenných sa vzorec pre aritmetický priemer môže odvodiť spočítaním súčinov každej premennej a jej frekvencie a výsledok sa potom vydelí súčtom frekvencií. Matematicky je reprezentovaný ako,
Arithmetic Mean = (f 1 *x 1 +f 2 *x 2 + …. + f n *x n ) / (f 1 + f 2 + ….. + f n )
alebo
Arithmetic Mean = ∑ (f i * x i ) / f i
Kde
- x i = i. premenná
- f i = Frekvencia i- tej premennej
Príklady aritmetického priemeru vzorca (so šablónou programu Excel)
Vezmime príklad, aby sme lepšie pochopili výpočet aritmetického priemeru.
Túto šablónu aritmetického priemeru vzorcov Excel si môžete stiahnuť tu - šablónu aritmetických priemerov vzorcov ExcelAritmetický stredný vzorec - príklad č. 1
Zoberme si príklad pálkara, ktorý zaznamenal v posledných 10 inningoch za posledný rok nasledujúce behy: 45, 65, 7, 10, 43, 35, 25, 17, 78, 91. Vypočítajte priemer batsmana za posledný rok 10 smien.
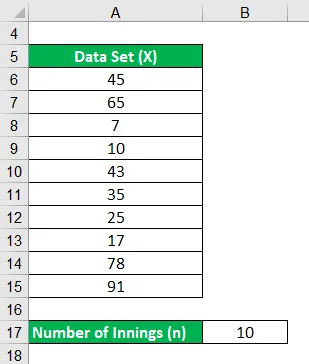
Riešenie:
Aritmetický priemer sa počíta pomocou vzorca uvedeného nižšie
Aritmetický priemer = ∑ x i / n
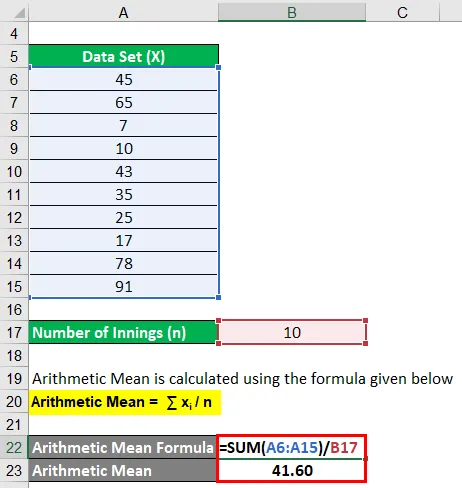
- Aritmetický priemer = (45 + 65 + 7 + 10 + 43 + 35 + 25 + 17 + 78 + 91) / 10
- Aritmetický priemer = 41, 60
Priemer batsmana teda zostal v posledných 10 inningoch 41, 60 behov na jednu směnu.
Aritmetický stredný vzorec - príklad č. 2
Ukážme príklad triedy so 45 študentmi. Nedávno sa uskutočňoval týždenný test pre vedu, v ktorom boli študenti hodnotení na stupnici od 1 do 10. Na základe nasledujúcich informácií vypočítajte priemerné známky v teste.
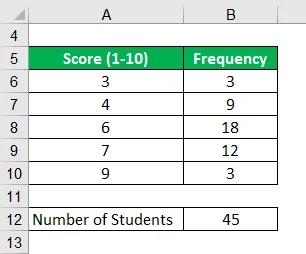
Riešenie:
Aritmetický priemer sa počíta pomocou vzorca uvedeného nižšie
Aritmetický priemer = ∑ (f i * x i ) / f i
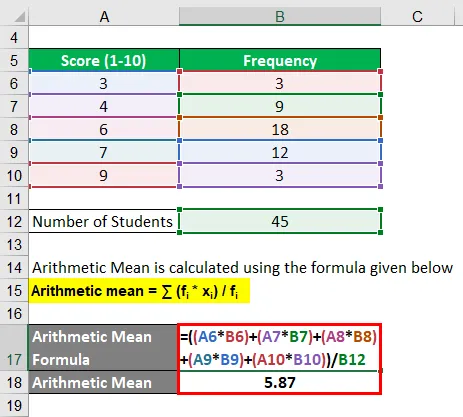
- Aritmetický priemer = ((3 * 3) + (4 * 9) + (6 * 18) + (7 * 12) + (9 * 3)) / 45
- Aritmetický priemer = 264/45
- Aritmetický priemer = 5, 87
Priemerné skóre triedy vo vedeckom teste preto bolo 5, 87.
Aritmetický stredný vzorec - príklad č. 3
Vezmime príklad dvoch súborov údajov s dvoma rôznymi aritmetickými prostriedkami. Prvý súbor údajov má 10 premenných s priemerom 45, zatiaľ čo druhý súbor údajov má 7 premenných a priemer 42. Stanovte aritmetický priemer oboch súborov údajov dohromady.
Riešenie:
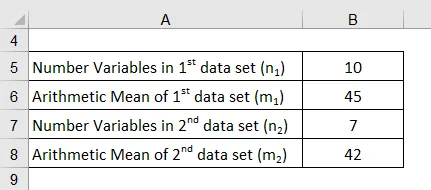
Aritmetické priemery kombinovaného súboru údajov sa vypočítajú pomocou vzorca uvedeného nižšie
Aritmetický priemer = ((m 1 * n 1 ) + (m 2 * n 2 )) / (n 1 + n 2 )
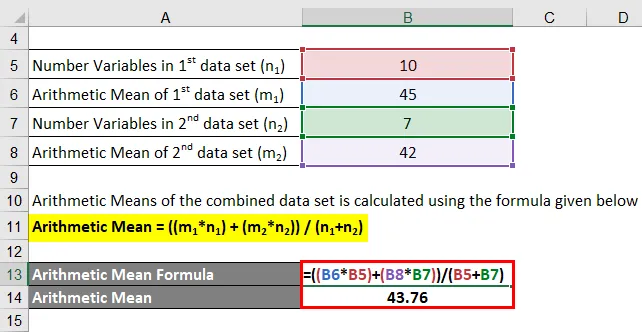
- Aritmetický priemer = (45 * 10 + 42 * 7) / (10 + 7)
- Aritmetický priemer = 43, 76
Aritmetický priemer kombinovaného súboru údajov je preto 43, 76.
vysvetlenie
Vzorec pre aritmetický priemer sa môže vypočítať pomocou nasledujúcich krokov:
Krok 1: Najprv zhromaždite a zoraďte premenné, pre ktoré sa musí vypočítať aritmetický priemer. Premenné sú označené x i .
Krok 2: Ďalej stanovte počet premenných v množine údajov a v prípade rovnako vážených premenných je označený ako n. V opačnom prípade určte frekvenciu každej premennej a označia sa fi a počet premenných predstavuje súčet frekvencií.
Krok 3: Konečne vzorec aritmetického priemeru pre rovnako vážené premenné možno odvodiť pridaním všetkých premenných a výsledok sa potom vydelí počtom premenných v súbore údajov, ako je uvedené nižšie.
Aritmetický priemer = ∑ x i / n
V prípade váženého priemeru sa však vzorec pre aritmetický priemer môže odvodiť spočítaním súčinov každej premennej a jej frekvencie a výsledok sa potom vydelí súčtom frekvencií, ako je uvedené nižšie.
Aritmetický priemer = ∑ f i * x i / f i
Relevantnosť a použitie aritmetického priemerného vzorca
Koncept aritmetického priemeru je veľmi jednoduchý a elementárny. Stále je však veľmi dôležitá, pretože sa často používa ako štatistický ukazovateľ na hodnotenie priemerného výsledku v súbore údajov. V skutočnosti umožňuje vyhodnotiť, ktoré z premenných sú lepšie alebo nižšie ako priemer skupiny. Používa sa tiež ako miera predstavujúca priemernú hodnotu v celom rade údajov. Aritmetický priemer sa ďalej používa v prípadoch, keď sú geometrické priemery alebo harmonické priemery menej užitočné, ako je priemerná známka, hmotnosť atď.
Aritmetický priemerný vzorec pre kalkulačku
Môžete použiť nasledujúcu aritmetickú priemernú kalkulačku
| x 1 | |
| x 2 | |
| x 3 | |
| x 4 | |
| n | |
| Aritmetický priemer | |
| Aritmetický priemer | = |
|
|
Odporúčané články
Toto je sprievodca aritmetickým priemerným vzorcom. Tu diskutujeme o tom, ako vypočítať aritmetický priemer spolu s praktickými príkladmi. Poskytujeme tiež aritmetický priemerný kalkulačka s možnosťou stiahnutia z Excel šablóny. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Ako vypočítať harmonický priemer?
- Sprievodca po strednom zložení obyvateľstva
- Výpočet strednej hodnoty pomocou vzorca
- Príklady vzorca čistého predaja