Vzorec priemernej hodnoty vlastného imania (obsah)
- Vzorec návratnosti priemerného kapitálu
- Kalkulačka návratnosti priemerného kapitálu
- Návratnosť priemernej hodnoty vlastného imania v Exceli (so šablónou Excelu)
Vzorec návratnosti priemerného kapitálu

Návratnosť priemerného vlastného imania sa vypočíta na určenie výkonnosti účtovnej jednotky. Vypočíta sa vydelením čistého príjmu priemerným vlastníkom akcií, kde „čistý zisk“ znamená čistý zisk rozdeliteľný medzi akcionárov vlastného imania, tj po odpočítaní všetkých výdavkov a platieb za pôžičky, dlhopisy a prioritné akcie a „priemerný kapitál akcionárov“ znamená priemer fondov akcionárov alebo peniaze vlastníka investované do podnikania v posledných dvoch rokoch.
Vo všeobecnej priemyselnej praxi sa návratnosť vlastného kapitálu používa výraznejšie ako návratnosť priemerného kapitálu. Návratnosť priemerného kapitálu však poskytuje lepšie pochopenie výkonnosti spoločnosti, najmä v prípade zmeny vlastného imania.
Príklady vzorca návratnosti priemerných akcií
Spoločnosť XYZ poskytla nasledujúce informácie na výpočet ROAE
Túto šablónu návratnosti priemerných akcií si môžete stiahnuť tu - šablóny návratnosti priemerných akcií- Čistý príjem za rok = Rs. 25, 000
- Vlastné imanie predchádzajúceho roku = Rs. 1, 00, 000
- Vlastné imanie bežného roka = Rs. 2, 00, 000
Poďme najprv vypočítať priemerný vlastný kapitál
- Priemerný vlastný kapitál = (vlastný kapitál za predchádzajúci rok + vlastný kapitál za bežný rok) / 2
- Priemerný vlastný kapitál = (1, 00 000 + 2, 00 000) / 2
- Priemerný vlastný kapitál = 1, 50 000
Teraz vypočítajme ROAE pre spoločnosť XYZ,
- ROAE = čistý príjem / priemerný vlastný kapitál
- ROAE = 25 000/1 50 000
- ROAE = 0, 1667 alebo 16, 67%
Vysvetlenie vzorca návratnosti priemerného kapitálu
Vzorec priemernej hodnoty vlastného kapitálu nám pomáha pochopiť, aký vysoký výnos generuje účtovná jednotka pre svojich akcionárov. Zjednodušene povedané, pomáha nám vypočítať, aký vysoký zisk vlastník akcií investuje do jednotky alebo koľko peňazí zarobil akcionár vlastného imania za každú rupiu, ktorú do nej vložil. Teraz by sa návratnosť vytvorená účtovnou jednotkou primerala alebo nelíšila od investora k investorovi na základe rizikovosti investície a iných alternatív investície. Napríklad, ak investor môže dosiahnuť návratnosť 7% - 8% zachovaním svojich peňazí v bankových fixných vkladoch, čo je relatívne menej riskantné z hľadiska návratnosti investície ako investície do vlastného imania účtovnej jednotky, potom očakávania investora z majetkovej účasti bude určite vyššia ako 7% - 8% a bude sa zvyšovať s vyššími rizikovými investíciami.
Keďže majitelia akcií sú poslednými osobami, ktoré majú účtovné jednotky zaplatiť po zaplatení všetkých výdavkov a splátok dlhov, riziko investovania kapitálového investora je vyššie ako iné v účtovnej jednotke, a teda aj jeho očakávanie vyššej návratnosti v porovnaní s dlhovými a preferenčnými akciami.,
Nie je však potrebné, aby zisky, ktoré sú k dispozícii na rozdelenie akcionárom, boli skutočne rozdelené. Účtovné jednotky sa môžu rozhodnúť rozdeliť časť zisku a zvyšok si ponechajú pre budúci rast.
Ako je uvedené v príklade vyššie, návratnosť priemerného vlastného imania sa teraz vypočíta vydelením čistého príjmu z predchádzajúceho roka s priemerným vlastným imaním z minulých 2 rokov, pričom čistý príjem predstavuje zisk po zdanení, ktorý je k dispozícii na rozdelenie akcionárovi vlastného imania, a prostriedky vlastného imania suma investovaná akcionármi vlastného imania.
Význam a využitie vzorca na výpočet priemernej hodnoty vlastného imania
Vzorec návratnosti priemerného kapitálu je významný pre investora, ktorý hodnotí investovanie do majetkových účastí spoločnosti, pretože pomocou tohto vzorca rozumie, aké výnosy môže od spoločnosti očakávať. ak sa rozhodnú investovať a potom ich porovnajú s inými alternatívnymi investíciami a výnosmi, aby urobili najlepšiu voľbu. Ak sa investori cítia byť riskantnou investíciou, môžu očakávať vyššiu návratnosť svojich investícií, a preto by mohli pomocou tohto vzorca skontrolovať, či spoločnosť niekedy poskytla druh návratnosti, ktorú očakáva, a či teda tvorí svoju / jej rozhodnutie investovať.
Vzorec návratnosti priemerného vlastného imania uvádza, že ako efektívne účtovná jednotka hospodári s peniazmi akcionárov. Ak je ukazovateľ na vyššej strane, znamenalo by to, že účtovná jednotka efektívne hospodári s peniazmi akcionára a ak je tento pomer na spodnej strane, je to náznak neefektívneho riadenia peňazí akcionárov a riadenia účtovnej jednotky.
Kalkulačka priemernej hodnoty návratnosti vlastného kapitálu
Môžete použiť nasledujúcu kalkulačku návratnosti priemernej hodnoty vlastného imania
| Čistý príjem | |
| Priemerný vlastný kapitál | |
| Vzorec návratnosti priemerného kapitálu (ROAE) | |
| Vzorec návratnosti priemerného kapitálu (ROAE) | = |
|
|
Návratnosť priemernej hodnoty vlastného imania v Exceli (so šablónou Excelu)
Tu urobíme rovnaký príklad vzorca návratnosti priemerných akcií v Exceli. Je to veľmi jednoduché a jednoduché. Musíte zadať dva vstupy: priemerný vlastný kapitál a čistý príjem
Vzorec Return On Average Equity Formula môžete ľahko vypočítať v poskytnutej šablóne.
Ako je znázornené v tabuľke, existuje spoločnosť s názvom VU, ktorej výpis z súvahy a výkazu ziskov a strát je uvedený, a musíme vypočítať návratnosť priemerného vlastného imania. Takže podľa vzorca sme najprv vypočítali čistý príjem, ktorý nie je ničím iným ako zisk po zdanení, a za týmto účelom odpočítame všetky náklady vrátane úrokov a odpisov od čistého predaja a dospejeme k zisku pred zdanením, potom odpočítame daň a dospieť k zisku po zdanení. Podobne sme v súvahe dostali dvojročnú sumu vlastného imania.
Najprv vypočítame priemerný vlastný kapitál
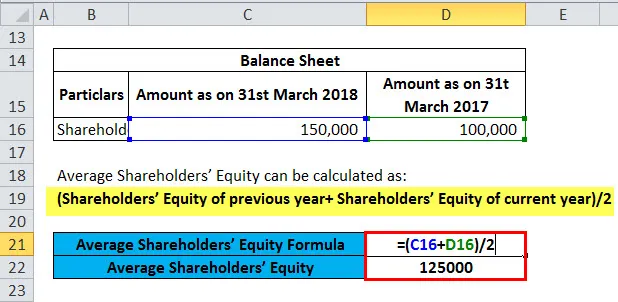
potom vypočítame návratnosť priemerného kapitálu pomocou vzorca

Odporúčané články
Bol to sprievodca vzorcom priemerných akcií, tu diskutujeme o jeho použitiach spolu s praktickými príkladmi. Poskytujeme vám tiež kalkulačku priemerných akcií spolu so stiahnuteľnou šablónou Excel.
- Vzorec hrubého zisku
- Vzorec multiplikátora vlastného imania
- Vzorec obratu pohľadávok
- Vzorec faktoru súčasnej hodnoty