Excel NORMSINV (obsah)
- Úvod do programu Excel NORMSINV
- Ako používať NORMSINV Formula v Exceli?
Úvod do programu Excel NORMSINV
Inverzná normálna kumulatívna distribučná funkcia v Exceli je dôležitým nástrojom, ktorý vracia inverznú normálnu kumulatívnu distribúciu pre danú pravdepodobnostnú hodnotu, tj normálne vracia inverznú inverziu k štandardnému normálnemu kumulatívnemu rozdeleniu (ktoré má strednú nulu a štandardnú odchýlku jednej). Funkcia NORM.S.INV bola prvýkrát predstavená v Microsoft Excel verzie 2010, ktorá je aktualizovanou verziou funkcie NORMSINV v Exceli 2013 a najnovšej verzii. Funkcia NORMSINV sa väčšinou používa v analýze záväzkov a financií.
Syntax programu Excel NORMSINV

argument:
Pravdepodobnosť - Čo nie je nič iné ako pravdepodobnosť zodpovedá normálnemu rozdeleniu.
Ako používať NORMSINV Formula v Exceli?
V programe Microsoft Excel je zabudovaná funkcia NORMSINV kategorizovaná do štatistickej funkcie, ktorá je uvedená na nasledujúcom snímke obrazovky (kde vypočíta inverziu normálneho kumulatívneho rozdelenia pre danú pravdepodobnosť).
- Prejdite do ponuky vzorcov.
- Kliknite na Viac funkcií, ako je to znázornené na nasledujúcom snímke obrazovky.

- Vyberte štatistickú kategóriu, pod ktorou nájdeme funkciu NORM.DIST, ako je uvedené nižšie.
Príklad č. 1 - Použitie NORM.DIST a NORMSINV
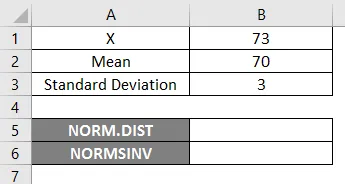
Aby sme mohli používať funkciu NORM.DIST, začnime jednoduchým príkladom, keď potrebujeme zistiť počet študentov, predpokladajme, že máme klasickú skúšku s priemerným stupňom 70 tj mu = 70 a štandardná odchýlka triedy je 3 body, tj sigma = 3. tu musíme zistiť, aká je pravdepodobnosť, že študenti získali známky 73 alebo nižšie, tj P (X <= 73). Pozrime sa, ako zistiť pravdepodobnosť pomocou funkcie NORM.DIST.
- X = 3
- Stredná = 70
- Štandardná odchýlka = 3
- Použite funkciu NORM.DIST ako je uvedené nižšie.
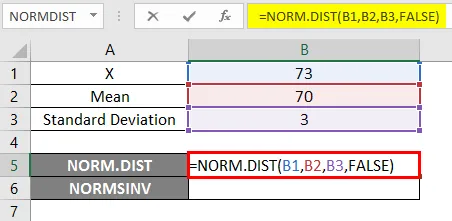
- Ak použijeme vyššie uvedenú funkciu NORM.DIST, dostaneme pravdepodobnosť 0, 0807.
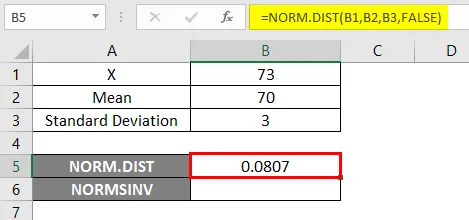
- Teraz použite funkciu NORMSINV a zistite inverziu normálneho kumulatívneho rozdelenia, ako je uvedené nižšie.
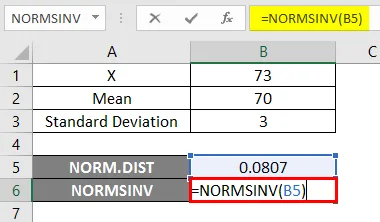
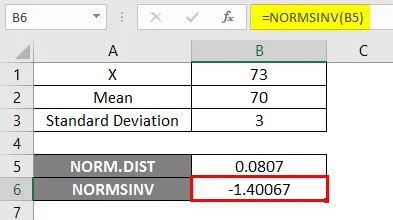
Výsledok -
V nižšie uvedenom výsledku vidíme, že sme dostali záporné hodnoty -1 40067 pre danú pravdepodobnosť, tj inverziu k normálnemu kumulatívnemu rozdeleniu.
Príklad č. 2 - Priemerná a presná štandardná odchýlka
Pozrime sa na ďalší príklad s údajmi založenými na krivkách, aby sme mohli spoznať priemernú a presnú štandardnú odchýlku.
- Priemer = 7
- Štandardná odchýlka = 1.3
- Štandardná odchýlka odchýlky ako -3

- Aby sme dostali zvonovú krivku, musíme k 0, 1 inkrementu odchýlky pridať štandardné odchýlky, kde sú údaje uvedené nižšie.
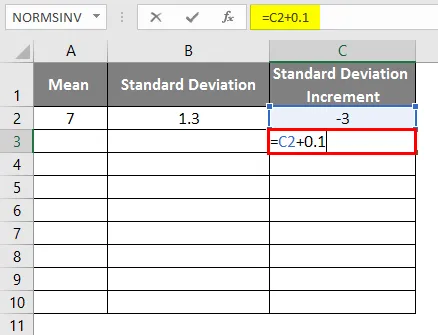
- Po použití vzorca je výsledok uvedený nižšie.
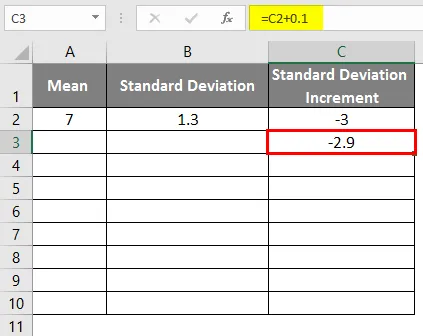
- Potiahnutím hodnôt získate ďalšie hodnoty, až kým nezískame kladné hodnoty, aby sme dostali ľavú krivku.
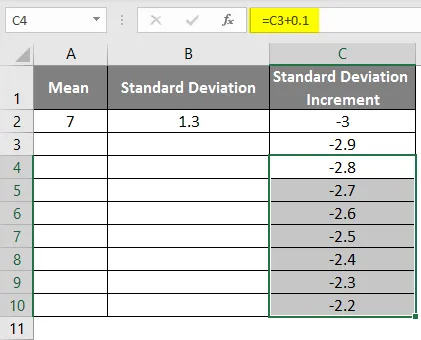
- Aby sme dostali pravú krivku, musíme použiť vzorec = stredná štandardná odchýlka * 3, aby sme dostali presné krivky.
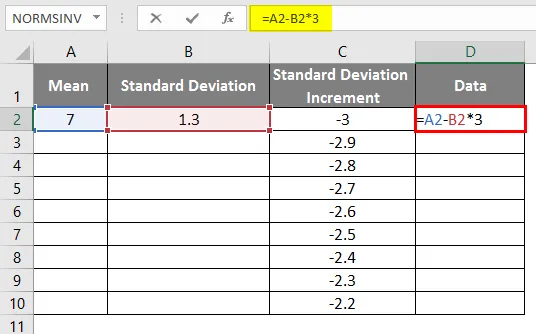
- Po použití vzorca je výsledok uvedený nižšie.
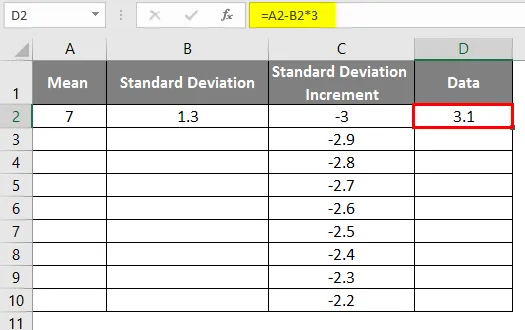
- Rovnako ako vo vyššie uvedených údajoch pre štandardný prírastok odchýlky na získanie ľavej krivky, hodnoty sme zvýšili o 0, 1
- Rovnaký scenár sa používa pri použití vzorca ako = 3, 1 + ŠTANDARDNÉ ROZVOJ / 10 na získanie prírastku krivky 0, 1
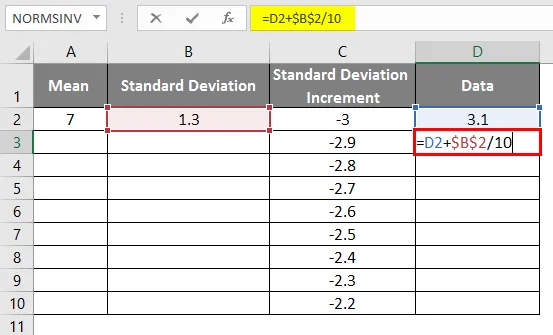
- Po použití vzorca je výsledok uvedený nižšie.

- Presunutím týchto hodnôt získate presný výsledok, ktorý je uvedený na nasledujúcom obrázku obrazovky.
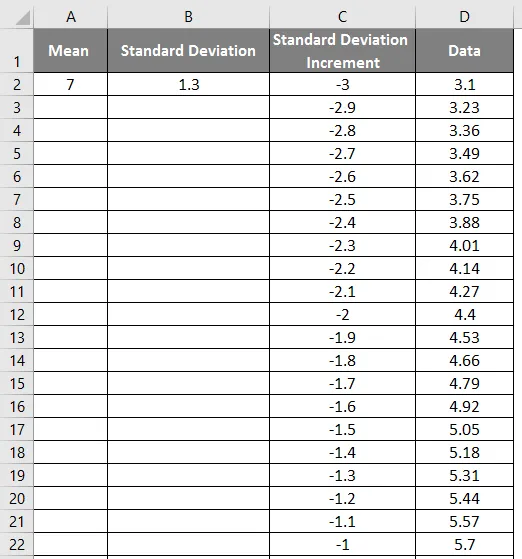
- Teraz použite funkciu normálneho rozdelenia pomocou vzorca = NORM.DIST (hodnota DATA, stredná hodnota, štandardná odchýlka, false).
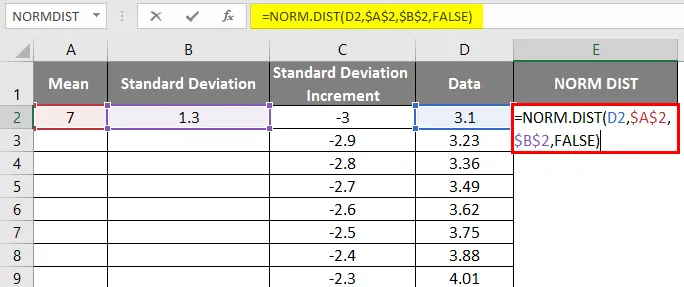
- Nižšie uvádzame výsledok.
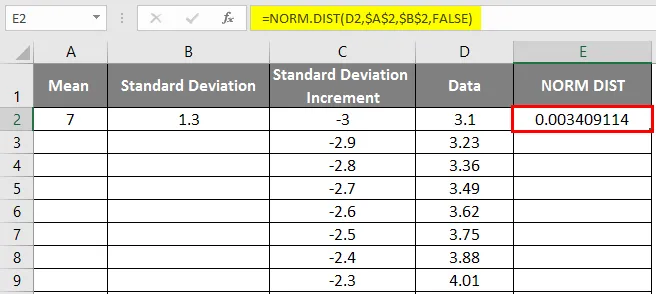
- Potiahnutím hodnôt získate presný výsledok, ktorý je uvedený nižšie.
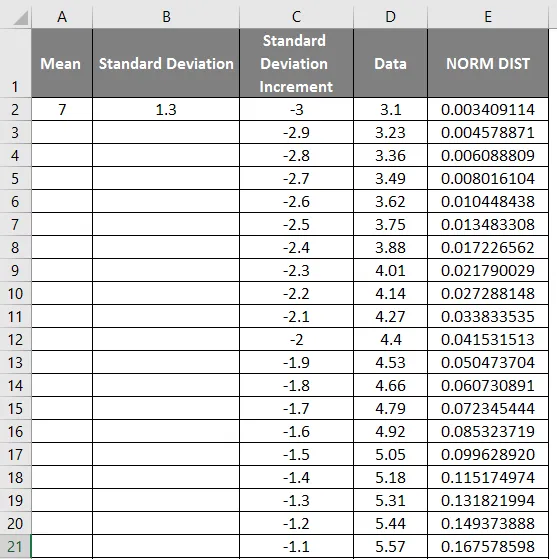
- Ako vidno na obrázku vyššie, vypočítali sme NORMÁLNE rozdelenie zo strednej a štandardnej odchýlky. Teraz sa pozrime, aká bude inverzia distribúcie NORMAL použitím NORMSINV, ktorý je uvedený nižšie.
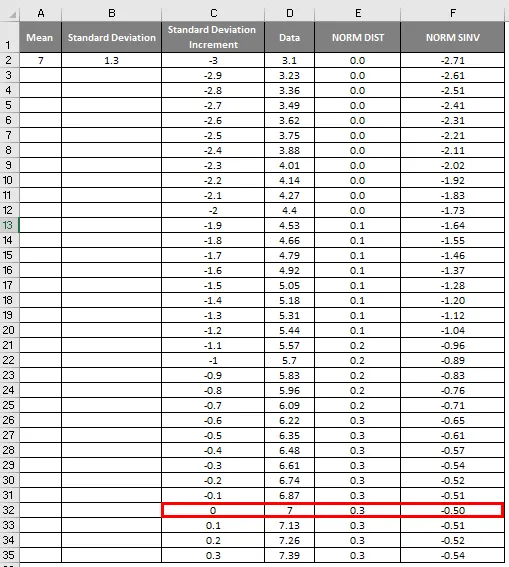
- Tu vidíme, že hodnota Zero (0) má štandardnú odchýlku 7.

Použitie rozptýleného grafu na pohľad na to, ako sa objaví ľavá a pravá krivka.
- Najskôr vyberte údaje a stĺpec Normálne.
- Prejdite na kartu Vložiť a nasledujúcim spôsobom vyberte rozptýlený graf.
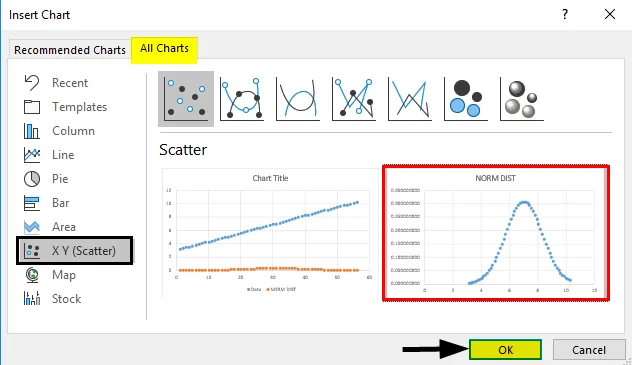
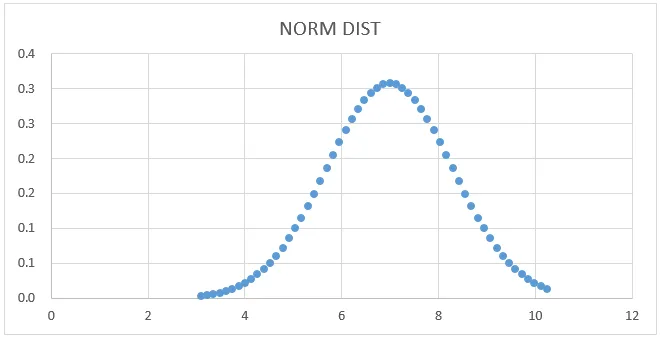
- Dostaneme nižšie uvedený graf krivky, ako je znázornené nižšie.
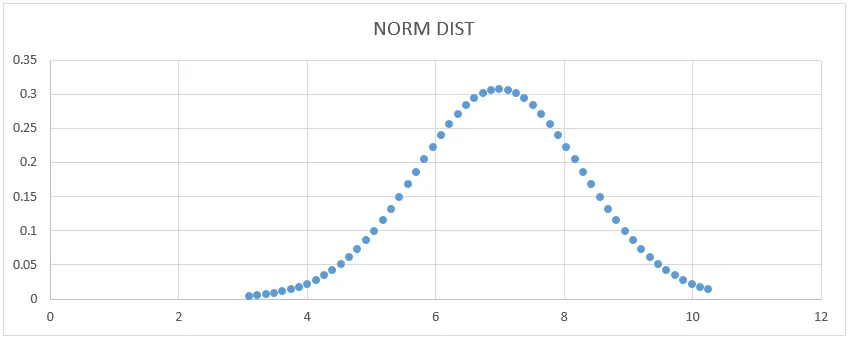
Tu vidíme, že stredná hodnota 7 má štandardný tvar odchýlky, kde môžeme ukázať, že nakreslením priamky, ktorá ju reprezentuje.
- Priemer = 7
- 1 - Štandardná odchýlka označuje 68% údajov.
- 2 - Štandardná odchýlka označuje 95% údajov.
- 3 - štandardná odchýlka označuje 99, 7% údajov.
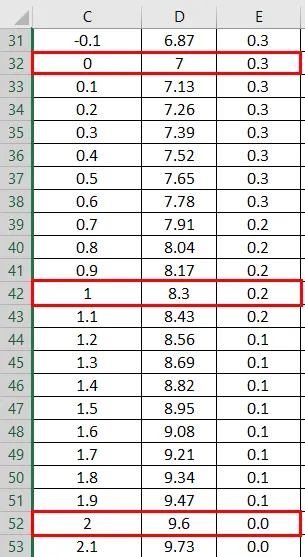
Graf normálneho rozdelenia:
Graf NORMSINV:
Teraz z vyššie uvedeného obrázku vyberte stĺpec s údajmi a NORM SINV, aby ste získali nižšie uvedený graf.
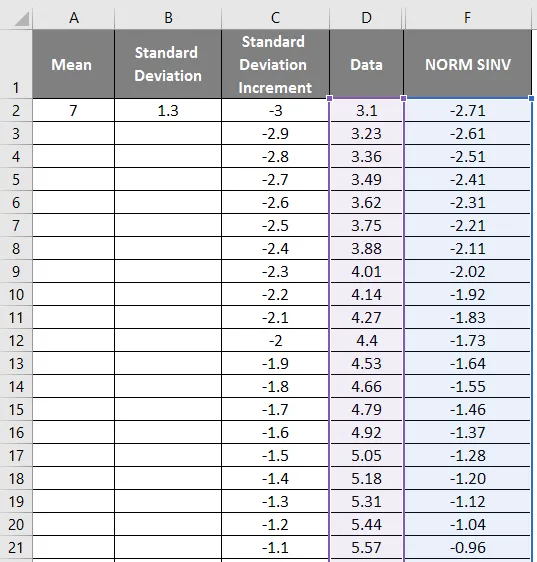
- Najskôr vyberte údaje a stĺpec Normálne.
- Prejdite na kartu Vložiť a vyberte rozptýlený graf.
- Dostaneme nižšie uvedený graf, ktorý je uvedený na nasledujúcom obrázku.
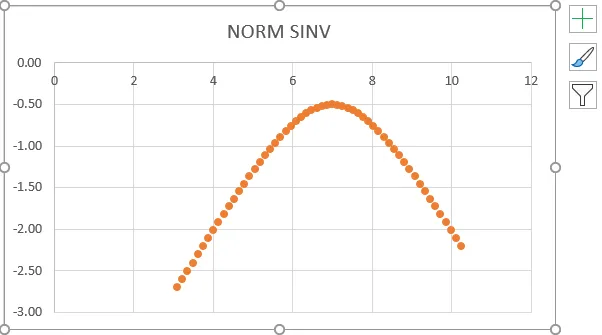
- Z vyššie uvedeného snímky obrazovky vidíme, že sme dostali presnú inverziu k normálnemu rozdeleniu, ktoré ukazuje rovnakú hodnotu hodnoty, ako je uvedené nižšie.

Príklad č. 3 - Konfigurácia ľavej a pravej krivky
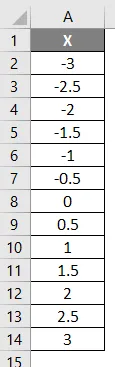
V tomto príklade nakonfigurujeme ľavú a pravú krivku pomocou funkcie normálneho rozdelenia. Zvážte nižšie uvedené údaje, ako je uvedené nižšie, kde x má záporné hodnoty a zvyšuje sa na kladné hodnoty.
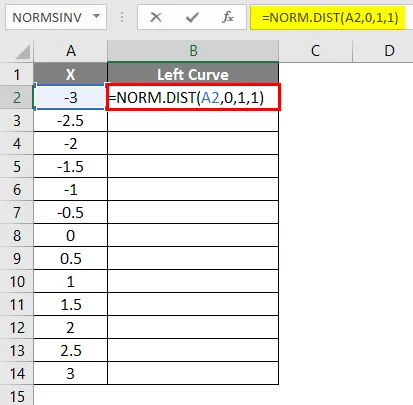
- Použite vzorec = NORM.DIST (A2, 0, 1, 1).
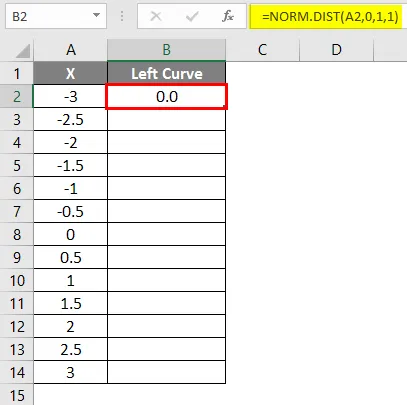
- Po použití vzorca je výsledok uvedený nižšie.
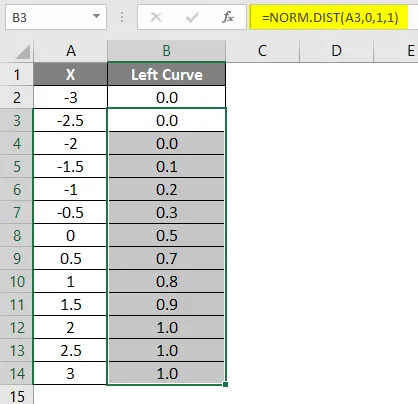
- Presuňte vzorec do iných buniek.
- Použite vzorec = 1-B2 .
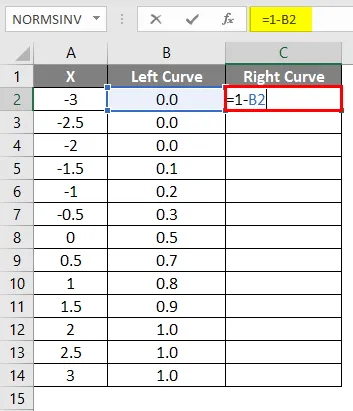
- Po použití vzorca je výsledok uvedený nižšie.
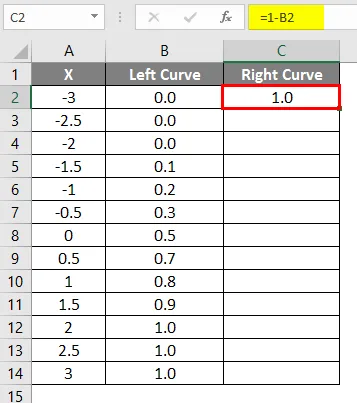
- Presuňte rovnaký vzorec do iných buniek.
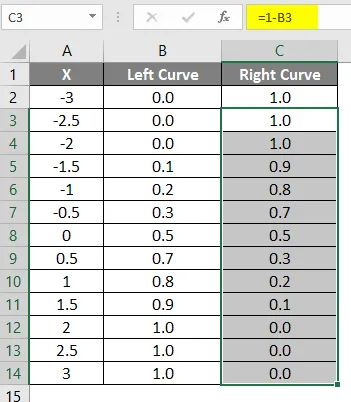
Výsledok vyššie uvedeného vzorca je uvedený nižšie.
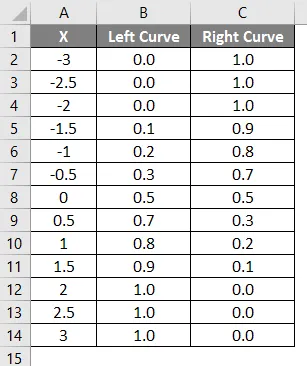
- Hodnoty ľavých kriviek boli vypočítané pomocou vzorca NORMÁLNA DISTRIBÚCIA nastavením kumulatívnej hodnoty ako True a hodnota NORMSINV bola vypočítaná pomocou ľavej krivky.
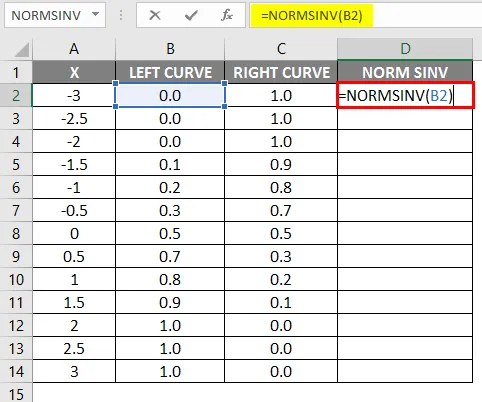
- Po použití vzorca je výsledok uvedený nižšie.
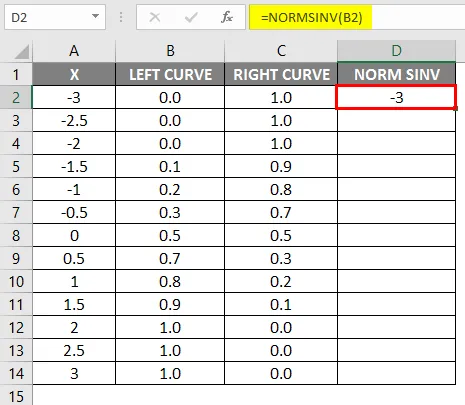
- Presuňte rovnaký vzorec do iných buniek.
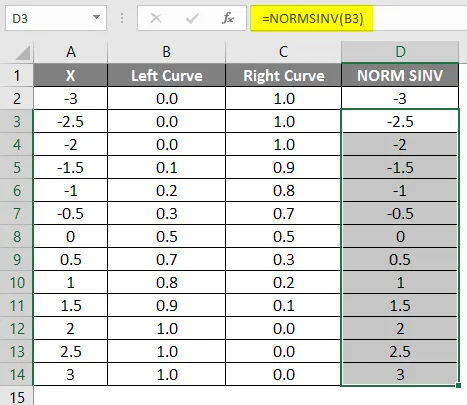
Ako vidíme, máme rovnakú hodnotu pre NORMSINV, čo nie je nič iné ako inverzia normálnej distribúcie. Rovnakým spôsobom získame správnu hodnotu krivky pomocou výpočtu hodnoty 1 krivky vľavo. V ďalšom kroku sa pomocou rozptýleného grafu skontrolujeme, ako dosiahneme výšku x.
- Vyberte stĺpec ľavá kúra a pravá krivka.
- Prejdite na ponuku vloženia.
- Vyberte rozptýlený graf nasledujúcim spôsobom.
Získame výsledok nižšie uvedeného grafu, ako je uvedené nižšie.
Graf NORM SINV:
V nasledujúcom grafe vidíme, že ľavá krivka hodnoty NORM DISTRIBÚCIA má presnú zhodu pre (0, 0, 5), ktorá leží v strede čiary, kde dostaneme rovnaký graf, ak požiadame o NORMDIST.
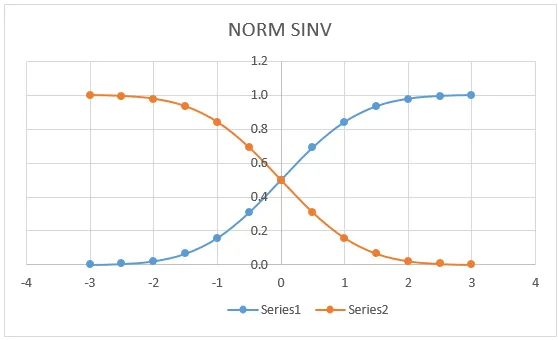
Tu vo vyššie uvedenom grafe veľmi jasne ukazuje, že presný priemer sme dostali v strede, ktorý označuje:
- X = 0
- Ľavá krivka = 0, 5
- Pravá krivka = 0, 5
Zobrazili sme ho na zobrazenie hodnôt NORMSINV v grafickom formáte, ako je uvedené nižšie.
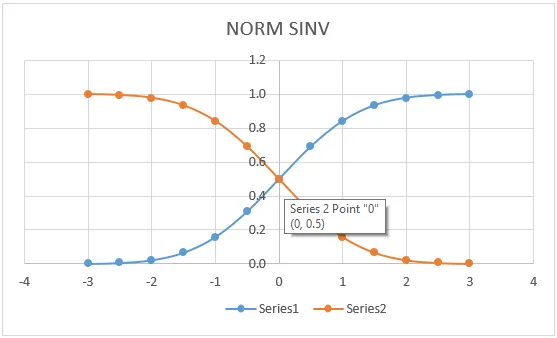
Čo je potrebné pamätať o aplikácii Excel NORMSINV
- # Hodnota! K chybe dôjde, ak daný argument nie je numerický alebo logický.
- Vo funkcii normálnej distribúcie zvyčajne dostaneme číslo # NUM! chyba kvôli argumentu smerodajnej odchýlky je menšia alebo rovná nule.
Odporúčané články
Toto je sprievodca Excelom NORMSINV. Tu diskutujeme o tom, ako používať NORMSINV v Exceli spolu s praktickými príkladmi a stiahnuteľnou vynikajúcou šablónou. Môžete si tiež prečítať naše ďalšie navrhované články -
- Ako používať meno v Exceli?
- Práca s Matrix v Exceli
- Čo keď analýza v Exceli
- Vzorec NPV v Exceli