Úvod do triedenia haldy v C
Triedenie je technika, ktorá sa týka usporiadania prvkov na základe rôznych vlastností. (Vlastnosti ako usporiadanie údajov vo vzostupnom, zostupnom alebo abecednom poradí). Jedným z hlavných príkladov triedenia, o ktorých tu vieme myslieť, je objednávanie položiek počas online nakupovania. Môžeme sa vzťahovať na ceny, popularitu, najnovšie a tak ďalej. Existuje teda veľa techník na umiestňovanie prvkov triedením. V tejto téme sa dozvieme viac o Heap Sort in C.
Tu sa naučíme jednu z najbežnejších metód triedenia, Heap Sort, prostredníctvom programovacieho jazyka C.
Logika pre usporiadanie haldy
Ako vlastne môžeme vykonať triedenie haldy? Poďme sa pozrieť nižšie.
Po prvé, halda je jednou zo stromovej štruktúry údajov. Tento strom je vždy kompletný binárny strom. A existujú dva druhy haldy
- Min. Hromada: Spravidla je usporiadaná vzostupne, to znamená, ak prvok nadradeného uzla má hodnotu nižšiu ako hodnota podriadených prvkov uzla.
- Max - Heap: Všeobecne usporiadané v zostupnom poradí, to znamená, ak má prvok nadradeného uzla hodnotu vyššiu ako hodnota prvkov podriadeného uzla.
Kroky pre triedenie haldy
- Akonáhle sa získajú netriedené zoznamové dáta, prvky sa usporiadajú do štruktúry údajov o halde buď na základe vytvorenia minimálnej alebo maximálnej úrovne.
- Prvý prvok z vyššie uvedeného zoznamu sa pridá do nášho poľa
- Opäť sa vytvorí technika štruktúry údajov o hlave, ktorá je rovnaká ako v prvom kroku, a opäť sa vyberie najvyšší prvok alebo najmenší prvok a pridá sa do nášho poľa.
- Opakované kroky nám pomáhajú získať pole so zoradeným zoznamom.
Program pre triedenie haldy v C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Najprv žiadame používateľa, aby vložil počet prvkov, ktoré sa použijú na triedenie, a potom môže užívateľ zadať rôzne prvky, ktoré sa majú triediť.
Nasledovali kroky
- Ďalej sa zameriavame na vytvorenie haldy, v tomto prípade max-haldy.
- Hlavnou podmienkou pre získanie poľa s maximálnou hodnotou haldy je skontrolovať, či žiadna hodnota nadradeného uzla nie je nižšia ako hodnota podradeného uzla. Budeme vymeniť, kým nedosiahneme túto podmienku.
- Hlavnou výhodou v tomto úplnom binárnom strome je, že k ľavému a pravému podriadenému uzlu nadradeného uzla je možné získať hodnoty 2 (i) + 1 a 2 * (i) + 2. Kde i je rodičovský uzol.
- Týmto spôsobom umiestnime náš koreňový uzol, ktorý obsahuje maximálnu hodnotu, na miesto na pravom listovom uzle. A potom znova podľa rovnakého postupu tak, že ďalšie maximálne číslo sa teraz stane koreňovým uzlom.
- Budeme postupovať rovnakým spôsobom, až kým v poli haldy nezostane iba jeden uzol.
- A potom usporiadame naše haldy do podoby dokonalého triedeného poľa v rastúcom poradí.
- Nakoniec tlačíme zoradené pole vo výstupe.
Výkon:
Výstup je pripojený nižšie.
Ukážem vám obrazové znázornenie udalostí:
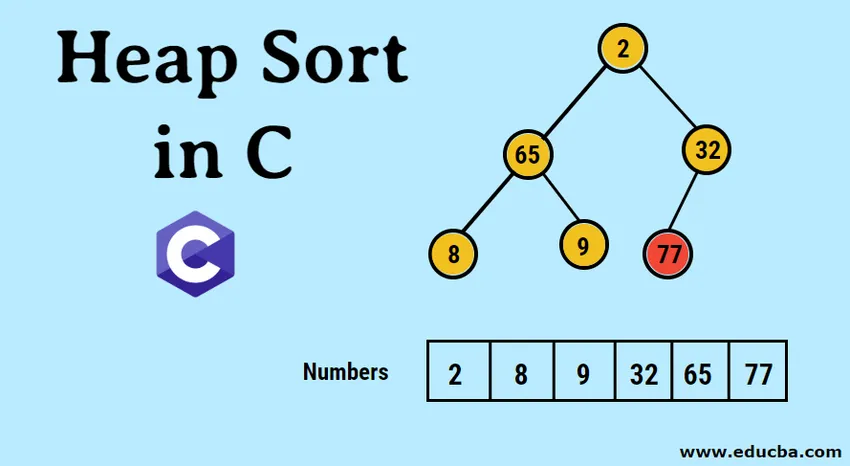
- Zadané údaje sa najprv reprezentujú vo forme jednorozmerného poľa nasledovne.

- Obrázková reprezentácia vytvoreného binárneho stromu je nasledovná:
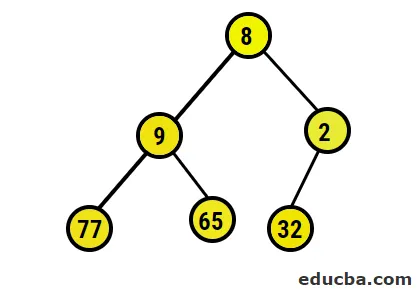
- Teraz sa chystáme prevádzať na maximálnu hromadu zabezpečením, aby všetky nadradené uzly boli vždy väčšie ako podradené uzly. Ako je uvedené vo výstupe v poli zoradenom podľa haldy, obrazová reprezentácia bude:
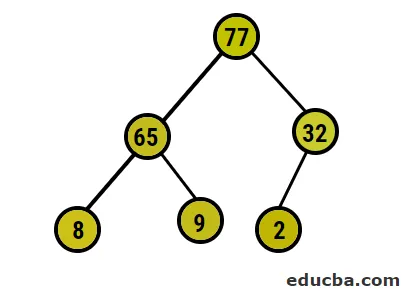
- Potom budeme zamieňať koreňový uzol za extrémny uzol listu a potom ho odstrániť zo stromu. Uzol listu by bol teraz koreňom a znova ten istý proces e, ktorý by opäť získal najvyšší prvok v koreňovom adresári
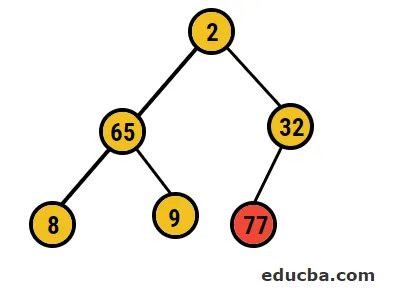
- V tomto prípade sa z tohto stromu odstráni 77 číslic a umiestni sa do nášho zoradeného poľa a proces sa opakuje.
Vyššie uvedené sme to videli pre formovanie max haldy poľa. Rovnakým procesom sa zaoberá aj tvorba poľa minovej hromady. Ako je uvedené vyššie, jediným rozdielom je vzťah medzi prvkami rodičovského a podriadeného uzla.
Ako cvičenie, môžete skúsiť formovať haldy v zostupnom poradí?
záver
Hoci existuje veľa triediacich techník, triedenie haldy je považované za jednu z lepších triediacich techník kvôli svojej časovej a priestorovej zložitosti. Časová zložitosť pre najlepší, priemerný a najhorší prípad je O (nlogn), kde najhoršia zložitosť je lepšia ako najhoršia zložitosť Quicksortu a zložitosť vesmíru je O (1).
Odporúčané články
Toto je sprievodca triedením haldy v C. Tu diskutujeme logiku a kroky pre triedenie haldy s ukážkovým kódom a výstupom spolu s obrázkovými znázorneniami. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Usporiadanie haldy v Jave
- Výber Zoradiť v Java
- Palindróm v programe C
- Vzory v programovaní C
- Usporiadanie haldy v C ++ (algoritmus)
- Halda Zoradiť v Pythone
- C násobenie programovacej matice