
Rozpätie chyby (obsah)
- Rozpätie chyby
- Príklady vzorcov marže chýb (so šablónou programu Excel)
- Rozpätie chybovej kalkulačky
Rozpätie chyby
V štatistike vypočítame interval spoľahlivosti, aby sme zistili, kde klesne hodnota údajov štatistických údajov. Rozsah hodnôt, ktoré sú pod a nad štatistikou vzorky v intervale spoľahlivosti, sa nazýva marža chyby. Inými slovami, v podstate ide o mieru chyby v štatistike vzorky. Čím vyššia je miera chybovosti, tým menšia bude dôvera vo výsledky, pretože miera odchýlky v týchto výsledkoch je veľmi vysoká. Ako už názov napovedá, miera chyby je rozsah hodnôt nad a pod skutočnými výsledkami. Napríklad, ak dostaneme odpoveď v prieskume, v ktorom 70% ľudí odpovedalo „dobre“ a miera chybovosti je 5%, znamená to, že všeobecne si 65% až 75% obyvateľstva myslí, že odpoveď je „dobrá“.,
Vzorec pre maržu chyby -
Margin of Error = Z * S / √n
Kde:
- Skóre Z - Z
- S - smerodajná odchýlka populácie
- n - Veľkosť vzorky
Ďalší vzorec na výpočet miery chyby je:
Margin of Error = Z * √((p * (1 – p)) / n)
Kde:
- p - Pomer vzorky (zlomok vzorky, ktorý je úspešný)
Teraz, aby ste našli požadované skóre z, musíte poznať interval spoľahlivosti vzorky, pretože na tom závisí skóre Z. Nasledujúca tabuľka uvádza vzťah intervalu spoľahlivosti a skóre z:
| Interval spoľahlivosti | Z - Skóre |
| 80% | 1, 28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2, 58 |
Akonáhle budete vedieť interval spoľahlivosti, môžete použiť zodpovedajúcu hodnotu z a vypočítať odchýlku chyby odtiaľ.
Príklady vzorcov marže chýb (so šablónou programu Excel)
Vezmime príklad, aby sme lepšie porozumeli výpočtu Margin of Error.
Túto šablónu marže chyby si môžete stiahnuť tu - šablónu marže chybyRozpätie chyby vzorec - príklad # 1
Povedzme, že robíme prieskum, aby sme zistili, aké je skóre bodov, ktoré dostávajú študenti vysokých škôl. Náhodne sme vybrali 500 študentov a požiadali sme ich o skóre. Priemer toho je 2, 4 zo 4 a smerodajná odchýlka je 30%. Predpokladajme, že interval spoľahlivosti je 99%. Vypočítajte mieru chyby.
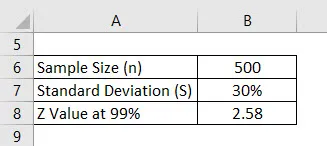
Riešenie:
Rozpätie chyby sa vypočíta pomocou vzorca uvedeného nižšie
Rozpätie chyby = Z * S / √n
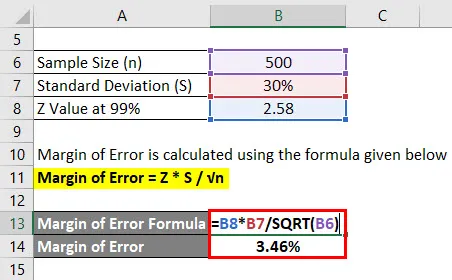
- Rozpätie chyby = 2, 58 * 30% / √ (500)
- Rozpätie chyby = 3, 46%
To znamená, že s 99% istotou je priemerná známka študentov 2, 4 plus alebo mínus 3, 46%.
Rozpätie chyby vzorec - príklad # 2
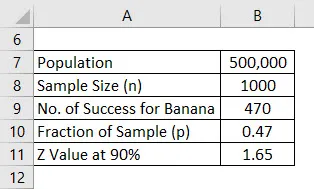
Povedzme, že uvádzate na trh nový zdravotnícky produkt, ale ste zmätení, akú chuť budú mať ľudia radi. Ste zmätení medzi príchuťou banánov a vanilkovou príchuťou a rozhodli ste sa vykonať prieskum. Vaša populácia pre to je 500 000, čo je váš cieľový trh, a z toho ste sa rozhodli opýtať sa na názor 1000 ľudí, a to bude vzorka. Predpokladajme, že interval spoľahlivosti je 90%. Vypočítajte mieru chyby.
Riešenie:
Po dokončení prieskumu ste zistili, že 470 ľudí chutilo banánovej chuti a 530 požiadalo o vanilkovú arómu.
Rozpätie chyby sa vypočíta pomocou vzorca uvedeného nižšie
Rozpätie chyby = Z * √ ((p * (1 - p)) / n)
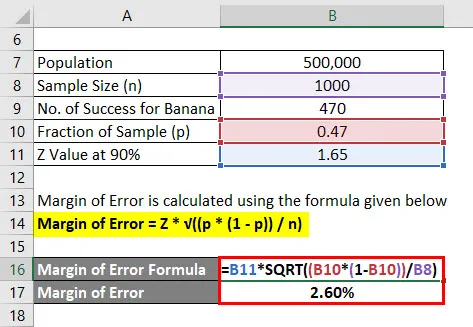
- Rozpätie chyby = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1 000)
- Rozpätie chyby = 2, 60%
Môžeme teda povedať, že s 90% istotou sa 47% všetkých ľudí páčilo s príchuťou banánov plus alebo mínus 2, 60%.
vysvetlenie
Ako je uvedené vyššie, miera chybovosti nám pomáha pochopiť, či je veľkosť vzorky vášho prieskumu primeraná alebo nie. V prípade, že je chyba okraja príliš veľká, môže sa stať, že veľkosť našej vzorky je príliš malá a musíme ju zvýšiť, aby sa výsledky vzorky lepšie zhodovali s výsledkami populácie.
Existujú niektoré scenáre, v ktorých sa miera chyby nebude veľmi využívať a nepomôže nám ju sledovať.
- Ak otázky z prieskumu nie sú navrhnuté a nepomáhajú získať požadovanú odpoveď
- Ak ľudia, ktorí odpovedajú na prieskum, majú určité skreslenie, pokiaľ ide o produkt, pre ktorý sa prieskum robí, potom výsledok tiež nemusí byť veľmi presný
- Ak je samotná vybraná vzorka vhodným zástupcom populácie, aj v tomto prípade budú výsledky ďaleko.
Veľkým predpokladom je aj to, že populácia je normálne distribuovaná. Takže ak je veľkosť vzorky príliš malá a distribúcia populácie nie je normálna, skóre z sa nedá vypočítať a nebudeme môcť nájsť hranicu chyby.
Relevancia a použitie rozpätia odchýlky
Kedykoľvek použijeme výberové údaje na nájdenie nejakej relevantnej odpovede pre súbor obyvateľov, existuje určitá neistota a šance, že sa výsledok môže líšiť od skutočného výsledku. Miera chyby nám povie, že aká je úroveň odchýlky, je tu výstup vzorky. Musíme minimalizovať mieru chýb, aby naše výsledky vzoriek zobrazovali skutočný príbeh údajov o populácii. Čím nižšia je miera chyby, tým lepšie budú výsledky. Miera chyby dopĺňa a dopĺňa štatistické informácie, ktoré máme. Napríklad, ak prieskum zistí, že 48% ľudí uprednostňuje trávenie času doma cez víkend, nemôžeme byť tak presní a v týchto informáciách sú niektoré chýbajúce prvky. Keď sme tu uviedli hranicu chýb, povedzme 5%, výsledok sa bude interpretovať tak, že 43-53% ľuďom sa myšlienka bytia cez víkend páčila, čo dáva zmysel.
Rozpätie chybovej kalkulačky
Môžete použiť nasledujúcu kalkulačku marže chýb
| Z | |
| S | |
| √n | |
| Rozpätie chyby | |
| Rozpätie chyby | = |
|
|
Odporúčané články
Toto bol sprievodca vzorcom Margin of Error. Tu diskutujeme o tom, ako vypočítať Margin of Error spolu s praktickými príkladmi. Poskytujeme tiež kalkulačku marže chýb s excelovateľnou šablónou na stiahnutie. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Sprievodca vzorcom odpisovania priamky
- Príklady vzorca zdvojnásobenia času
- Ako vypočítať amortizáciu?
- Vzorec pre centrálnu limitnú vetu
- Skóre Altman Z | Definícia Príklady
- Odpisový vzorec Príklady so šablónou programu Excel