
Úvod do binomického rozdelenia v R
Tento článok popisuje, ako používať binomické distribúcie v R pre niekoľko operácií spojených s distribúciou pravdepodobnosti. Business Analysis využíva binomickú pravdepodobnosť pre komplexný problém. R má početné vstavané funkcie na výpočet binomického rozdelenia použitého pri štatistickej interferencii. Binomické rozdelenie známe tiež ako Bernoulliho skúšky trvá dva typy úspechu p a zlyhanie S. Hlavným cieľom modelu binomického distribúcie je, že vypočítajú možné výsledky pravdepodobnosti sledovaním konkrétneho počtu pozitívnych možností opakovaním procesu konkrétnym počtom opakovaní., Mali by mať dva možné výsledky (úspech / zlyhanie), a preto je výsledok dichotomický. Preddefinovaná matematická notácia je p = úspech, q = 1-p.
S binomickým rozdelením sú spojené štyri funkcie. Sú to dbinom, pbinom, qbinom, rbinom. Formátovaná syntax je uvedená nižšie:
syntax
- dbinom (x, veľkosť, prob)
- pbinom (x, veľkosť, prob)
- qbinom (x, veľkosť, prob) alebo qbinom (x, veľkosť, prob, low_tail, log_p)
- rbinom (x, veľkosť, prob)
Funkcia má tri argumenty: hodnota x je vektor kvantilov (od 0 do n), veľkosť je počet pokusov o stopu, pravdepodobnosť označuje pravdepodobnosť každého pokusu. Pozrime sa jeden na druhého s príkladom.
1) dbinom ()
Je to funkcia hustoty alebo distribúcie. Hodnoty vektora musia byť celé číslo, nemalo by byť záporné číslo. Táto funkcia sa pokúša nájsť rad úspechov v čísle. pokusov, ktoré sú stanovené.
Binomické rozdelenie má hodnoty veľkosti x. napríklad veľkosť = 6, možné hodnoty x sú 0, 1, 2, 3, 4, 5, 6, čo znamená P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Výkon:
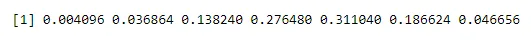
Zvýšenie pravdepodobnosti na jeden
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Výkon:
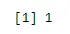
Príklad 1 - Databáza nemocníc ukazuje, že pacienti trpiaci na rakovinu zomierajú na ňu 65%. Aká je pravdepodobnosť pravdepodobnosti 5 náhodne vybraných pacientov, z ktorých sa 3 zotavia?
Tu aplikujeme funkciu dbinom. Pravdepodobnosť, že 3 sa získa pomocou distribúcie hustoty vo všetkých bodoch.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Výkon:

Pre hodnotu x 0 až 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Výkon:
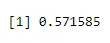
Ďalej vytvorte vzorku 40 papierov a zvýšite o 2 a vytvorte tiež binomické dbinom.
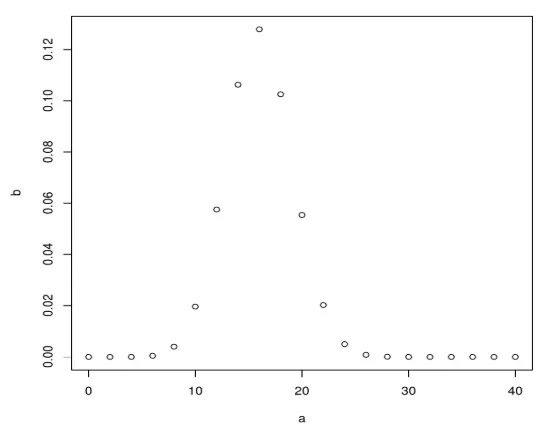
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
Po vykonaní vyššie uvedeného kódu vytvorí nasledujúci výstup. Binomické rozdelenie je vynesené pomocou funkcie plot ().
Príklad 2 - Zoberme si scenár, predpokladajme, že pravdepodobnosť, že si študent požičia knihu z knižnice, je 0, 7. V knižnici je 6 študentov, aká je pravdepodobnosť, že 3 z nich požičia knihu?
tu P (X = 3)
kód:
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
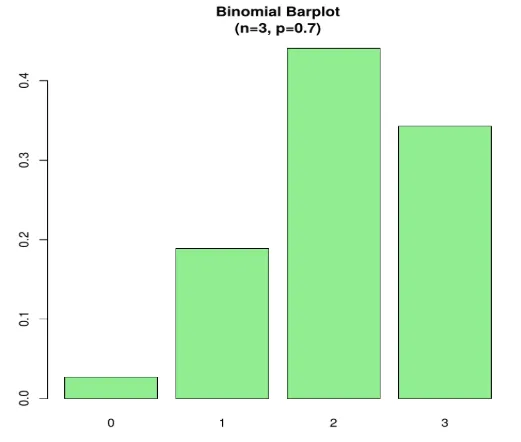
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Pod Plot zobrazuje, keď p> 0, 5, preto je binomické rozloženie pozitívne nakreslené, ako je zobrazené.
Výkon:
2) Pbinom ()
vypočíta kumulatívne pravdepodobnosti binomického alebo CDF (P (X <= x)).
Príklad 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Výkon:

Príklad 2: Dravid skóruje bránku na 20% svojich pokusov, keď sa pokúša. Ak sa bude päťkrát hádzať, aká by bola pravdepodobnosť, že dosiahne 4 alebo menej bránky?
Pravdepodobnosť úspechu je tu 0, 2 a počas 5 pokusov dostaneme
pbinom(4, size=5, prob=.2)
Výkon:
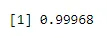
Príklad 3: 4% Američanov sú čierni. Nájdite pravdepodobnosť 2 čiernych študentov pri náhodnom výbere 6 študentov zo triedy 100 bez náhrady.
Keď R: x = 4, R: n = 6, R: p = 0, 04
pbinom(4, 6, 0.04)
Výkon:-
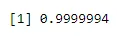
3) qbinom ()
Je to kvantová funkcia a robí inverznú funkciu kumulatívnej pravdepodobnosti. Kumulatívna hodnota sa zhoduje s pravdepodobnosťou.
Príklad: Koľko chvostov bude mať pravdepodobnosť 0, 2, keď sa minca hodí 61-krát.
a <- qbinom(0.2, 61, 1/2)
print(a)
Výkon:-
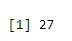
4) rbinom ()
Generuje náhodné čísla. Rôzne výstupy vytvárajú rôzne náhodné výstupy, ktoré sa používajú v simulačnom procese.
Príklad: -
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Výkon:-

Zakaždým, keď to vykonáme, dáva náhodné výsledky.
rbinom(200, 4, 0.4)
Výkon:-

Urobíme to tak, že pri jednom pokuse budeme vychádzať z výsledku 30 vyhodených mincí.
rbinom(30, 1, 0.5)
Výkon:-
Použitie barplot:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Výkon:-
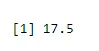
Nájsť spôsob úspechu
output <-rbinom(10, size=60, 0.3)
mean(output)
Výkon:-
Záver - Binomické rozdelenie v R.
Preto sme v tomto dokumente diskutovali o binomickom rozdelení v R. Simulovali sme pomocou rôznych príkladov v R štúdiu a útržkoch R a tiež sme opísali zabudované funkcie, ktoré pomáhajú pri generovaní binomických výpočtov. Výpočet binomického rozdelenia v R používa štatistické výpočty. Preto binomické rozdelenie pomáha pri hľadaní pravdepodobnosti a náhodného vyhľadávania pomocou binomickej premennej.
Odporúčané články
Toto je príručka k binomickému rozdeleniu v R. Tu sme diskutovali úvod a jeho funkcie spojené s binomickým rozdelením spolu so syntaxou a príslušnými príkladmi. Viac informácií nájdete aj v ďalších navrhovaných článkoch -
- Binomický distribučný vzorec
- Ekonomika verzus podnikanie
- Techniky obchodnej analýzy
- Distribúcie systému Linux