
R - Štvorcový vzorec (obsah)
- R - štvorcový vzorec
- Príklady vzorca R - druhá mocnina (so šablónou programu Excel)
- R - štvorcová kalkulačka
R - štvorcový vzorec
Vzorec s druhou mocninou je tiež známy ako koeficient určenia, je to štatistické opatrenie, ktoré určuje koreláciu medzi výkonnosťou investora a výnosom alebo výkonnosťou referenčného indexu. V podstate ukazuje, do akej miery možno výkonnosť akcií alebo portfólia pripísať konkrétnemu referenčnému indexu. Tento vzorec sa mierne líši od korelácie premennej, pretože korelačný vzorec ukazuje vzťah medzi závislou a nezávislou premennou, zatiaľ čo na druhej strane vzorec R-ssvetlený ukazuje, do akej miery rozptyl jednej premennej vysvetľuje rozptyl druhej premennej.,
Vzorec pre R - Squared je daný:
R – Squared = 1 – (Sum of First Errors / Sum of Second Errors)
Príklady vzorca R - druhá mocnina (so šablónou programu Excel)
Vezmime príklad, aby sme lepšie porozumeli výpočtu R - Squared.
Túto šablónu vzorcov R - Squared si môžete stiahnuť tu - šablónu vzorcov R - Squared FormulaPríklad č. 1
Zvážte nasledujúce informácie a vypočítajte R na druhú.
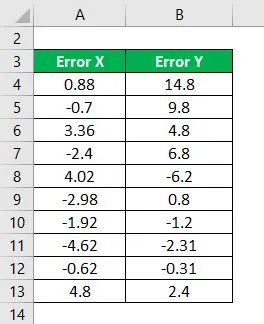
Štvorec chyby X sa vypočíta ako:
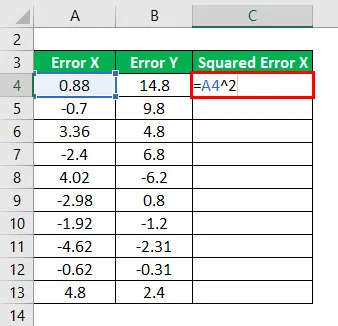
Výsledok bude uvedený nižšie.
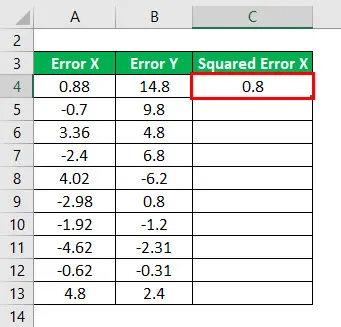
Štvorec chyby X pre všetky údaje, ako je uvedené nižšie.
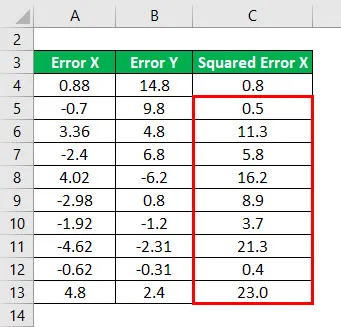
Podobne musíme pre všetky údaje vypočítať druhú mocninu Y.
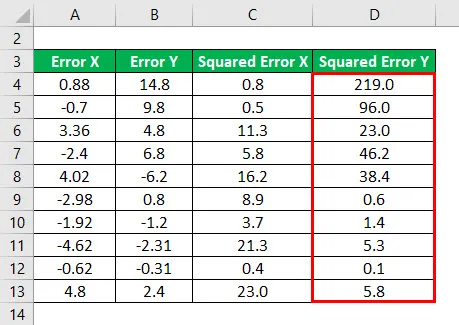
R - druhá mocnina sa vypočíta pomocou vzorca uvedeného nižšie
R - na druhú stranu = 1 - (súčet prvých chýb / súčet druhých chýb)
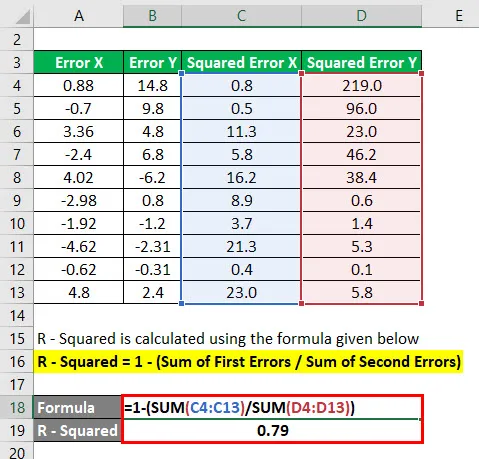
Najprv sme na druhú stranu určili chybu v nasledujúcich bodoch a urobili sme zhrnutie vyššie uvedených problémov. Potom sa súčet prvej chyby vydelí súčtom druhej chyby a odpočíta sa 1.
R-kvadrát leží v rozmedzí 0 až 1. Hodnota r-kvadratická odchýlka 1 alebo 100% znamená, že všetky pohyby v indexe sú úplne vysvetlené pohybmi v referenčnom indexe.
Príklad č. 2
Zvážte nasledujúce informácie a vypočítajte R na druhú.
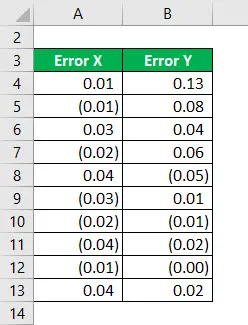
Štvorec chyby X sa vypočíta ako:
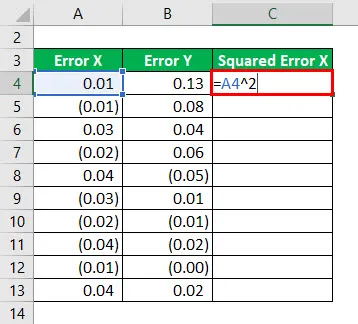
Výsledok bude uvedený nižšie.
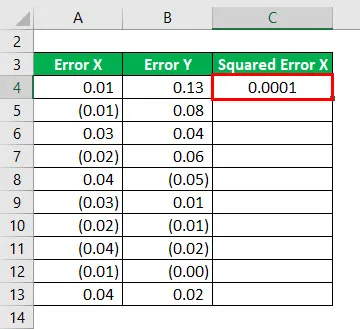
Druhá mocnina chyby X pre všetky údaje, ako je uvedené nižšie.
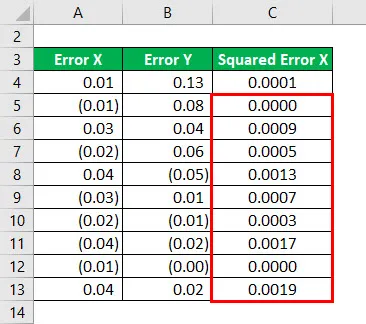
Podobne musíme vypočítať druhú mocninu chyby Y pre všetky údaje.
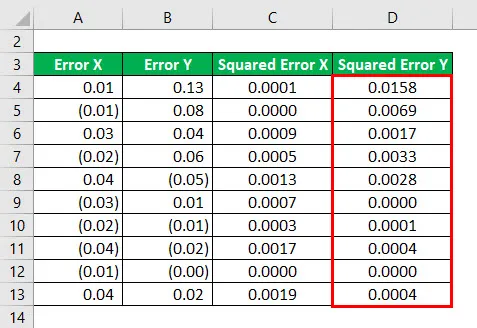
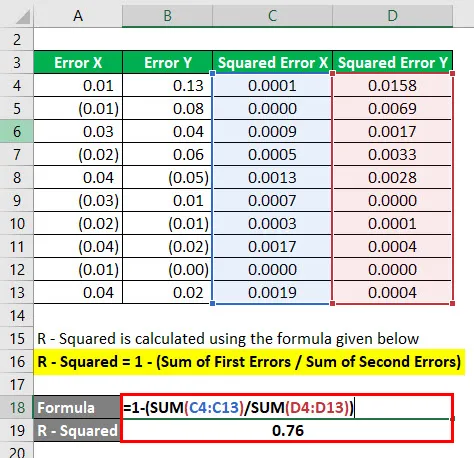
R - druhá mocnina sa vypočíta pomocou vzorca uvedeného nižšie
R - na druhú stranu = 1 - (súčet prvých chýb / súčet druhých chýb)
Príklad č. 3
Zvážte nasledujúce informácie a vypočítajte R na druhú.
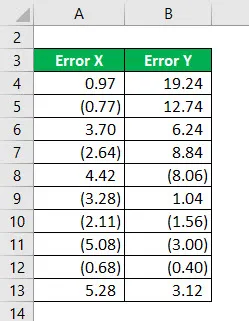
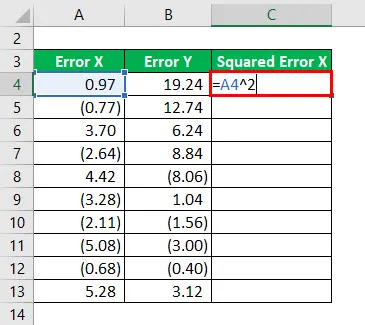
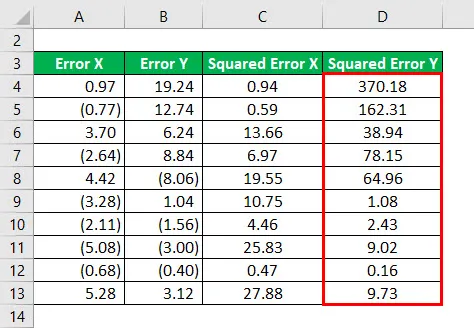
Druhá mocnina chyby X sa vypočíta ako:
Výsledok bude uvedený nižšie.
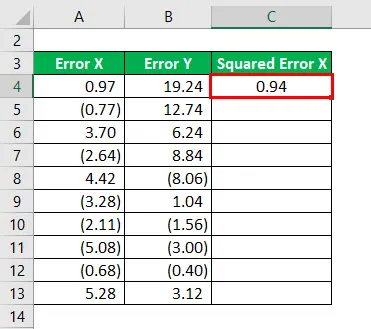
Druhá mocnina chyby X pre všetky údaje, ako je uvedené nižšie.
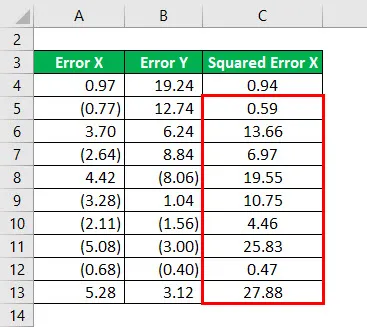
Podobne musíme vypočítať druhú mocninu chyby Y pre všetky údaje.
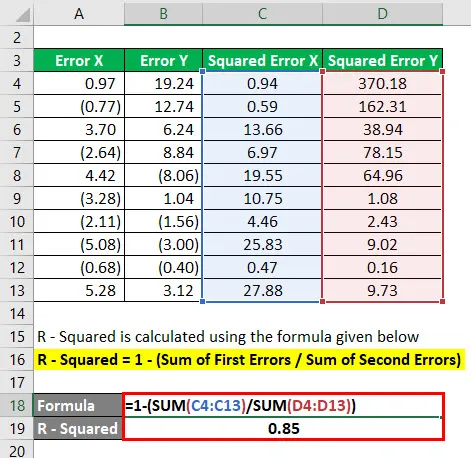
R - druhá mocnina sa vypočíta pomocou vzorca uvedeného nižšie
R - na druhú stranu = 1 - (súčet prvých chýb / súčet druhých chýb)
Relevantnosť a použitia
- Tento vzorec často používajú manažéri portfólia a správcovia fondov ako opatrenie, ktoré hovorí o tom, ako pohyby fondov korelujú s referenčným indexom.
- Tento vzorec sa používa aj v priemysle na akciových trhoch, ktorý hovorí maklérovi alebo investorovi o tom, ako dobre akcie korelujú s celkovým pohybom trhu.
- Tento vzorec má svoje vlastné obmedzenia, pretože nedokáže posúdiť, či sú odhady koeficientov a predpovede skreslené alebo nie, a preto je potrebné posúdiť iba zvyškové grafy.
- Tam, kde R - Squared neslúži ako dobrý porovnávací model na porovnanie dobra oboch premenných, R-Squared upravené sa väčšinou používa na vykonanie viacerých lineárnych regresií.
- Nízke alebo vysoké R na druhú mocninu nemôže byť vždy dobré alebo zlé, pretože to užívateľovi nehovorí o spoľahlivosti modelu.
- Ak má užívateľ nízku hodnotu na druhú mocninu, ale nezávislé premenné sú štatisticky významné, môže si ešte stále vyvodiť dôležité závery o vzťahoch medzi premennými.
R - štvorcová kalkulačka
Môžete použiť nasledujúcu kalkulačku R - Squared
| Súčet prvých chýb | |
| Súčet druhých chýb | |
| R - štvorcový vzorec | |
| R - druhá mocnina = | 1 - (Súčet prvých chýb / Súčet druhých chýb) |
| = | 1 - (0/0) = 0 |
Odporúčané články
Toto bol sprievodca po R - Squared Formula. Tu diskutujeme o tom, ako vypočítať R - Squared spolu s praktickými príkladmi. Poskytujeme tiež kalkulačku R - Squared s vynikajúcou šablónou na stiahnutie. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Sprievodca vzorcom očakávaného návratu
- Ako vypočítať pomer PEG?
- Príklady vzorca pre pomer solventnosti
- Kalkulačka pre pomer pákového efektu