
Vzorec efektívnej úrokovej miery (obsah)
- vzorec
- Príklady
- kalkulačka
Čo je vzorec efektívnej úrokovej sadzby?
Pojem „efektívna úroková miera“ sa vzťahuje na skutočný ročný výnos investície, ktorý sa získa vďaka výsledku zloženia za určité časové obdobie. Naopak, efektívna úroková miera sa dá považovať za skutočné náklady na pôžičku z pohľadu dlžníka. Je tiež známa ako skutočná ročná návratnosť alebo ročná ekvivalentná sadzba. Vzorec pre efektívnu úrokovú sadzbu možno odvodiť na základe stanovenej úrokovej sadzby a počtu období zloženia za rok. Matematicky je reprezentovaný ako,
Effective Interest Rate = (1 + i/n) n – 1
kde,
- i = Uvedená úroková miera
- n = počet období zloženia za rok
Príklady vzorca efektívnej úrokovej sadzby (so šablónou programu Excel)
Vezmime príklad, aby sme lepšie pochopili výpočet efektívnej úrokovej sadzby.
Túto šablónu efektívnej úrokovej miery vzorca Excel si môžete stiahnuť tu - šablónu efektívnej úrokovej miery vzorca ExcelVzorec efektívnej úrokovej sadzby - príklad č. 1
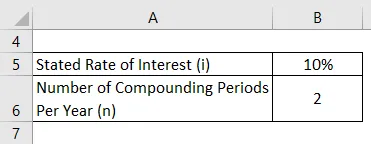
Zoberme si príklad investície s uvedenou úrokovou sadzbou 10%. Vypočítajte efektívnu úrokovú sadzbu, ak sa má investovať dvakrát do roka.
Riešenie:
Efektívna úroková sadzba sa vypočíta pomocou vzorca uvedeného nižšie
Efektívna úroková sadzba = (1 + i / n) n - 1

- Efektívna úroková miera = (1 + 10% / 2) 2 - 1
- Efektívna úroková miera = 10, 25%
Efektívna úroková sadzba pre kótovanú investíciu je preto 10, 25%.
Vzorec efektívnej úrokovej sadzby - príklad č. 2
Zoberme si príklad Johna, ktorý má záujem investovať dlhopis, ktorý ponúka uvedenú úrokovú sadzbu 9%. Povaha zloženia je však iná a John si nie je istý, ktoré zloženie prinesie najvyšší výnos. Vypočítajte efektívnu úrokovú sadzbu a pomôžte Johnovi urobiť plodné rozhodnutie pre nasledujúce obdobie zloženia:
- Výročný
- polročná
- štvrťročné
- mesačník
- denná
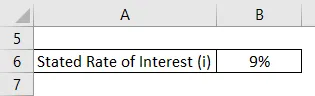
Výročný
Efektívna úroková sadzba sa vypočíta pomocou vzorca uvedeného nižšie
Efektívna úroková sadzba = (1 + i / n) n - 1
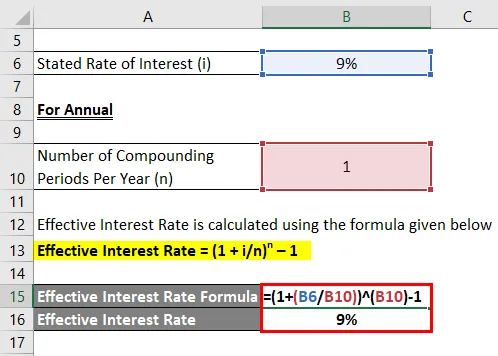
- Efektívna úroková miera = (1 + 9% / 1) 1 - 1
- Efektívna úroková sadzba = 9%
polročná
Efektívna úroková sadzba sa vypočíta pomocou vzorca uvedeného nižšie
Efektívna úroková sadzba = (1 + i / n) n - 1
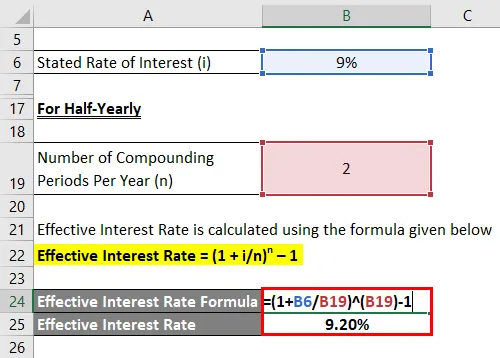
- Efektívna úroková miera = (1 + 9% / 2) 2 - 1
- Efektívna úroková sadzba = 9, 20%
štvrťročné
Efektívna úroková sadzba sa vypočíta pomocou vzorca uvedeného nižšie
Efektívna úroková sadzba = (1 + i / n) n - 1
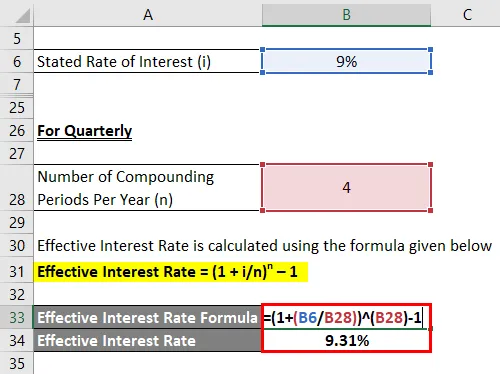
- Efektívna úroková miera = (1 + 9% / 4) 4 - 1
- Efektívna úroková sadzba = 9, 31%
mesačník
Efektívna úroková sadzba sa vypočíta pomocou vzorca uvedeného nižšie
Efektívna úroková sadzba = (1 + i / n) n - 1
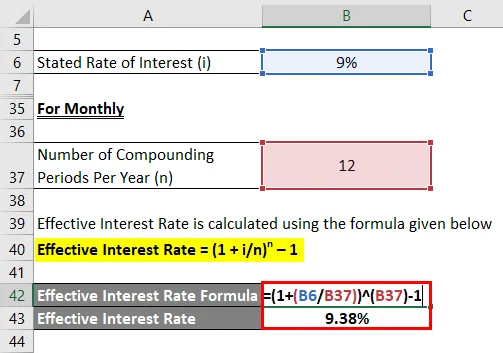
- Efektívna úroková miera = (1 + 9% / 12) 12 - 1
- Efektívna úroková miera = 9, 38%
denná
Efektívna úroková sadzba sa vypočíta pomocou vzorca uvedeného nižšie
Efektívna úroková sadzba = (1 + i / n) n - 1

- Efektívna úroková miera = (1 + 9% / 365) 365 - 1
- Efektívna úroková miera = 9, 42%
Preto je možné jasne vidieť, že ročný výnos sa zvyšuje so zvyšujúcim sa počtom zložení ročne. Preto možnosť denného kombinovania ponúkne najlepší výnos pre Johna (efektívny úrok 9, 38% oproti stanovenej úrokovej sadzbe 9%).
vysvetlenie
Vzorec pre efektívnu úrokovú sadzbu možno odvodiť pomocou nasledujúcich krokov:
Krok 1: Najskôr určte uvedenú úrokovú sadzbu investície, ktorá je zvyčajne uvedená v investičnom dokumente. Označuje sa „i“.
Krok 2: Ďalej zistite počet kombinovaných období počas roka a označuje sa „n“. Spravidla sa zmiešavanie uskutočňuje štvrťročne, polročne a ročne, čo znamená počet zložení za rok 4, 2 a 1.
Krok 3: Konečne vzorec pre efektívnu úrokovú sadzbu možno odvodiť s použitím uvedenej úrokovej sadzby (krok 1) a niekoľkých zložených období za rok (krok 2), ako je uvedené nižšie.
Efektívna úroková sadzba = (1 + i / n) n - 1
Relevantnosť a použitie vzorca efektívnej úrokovej sadzby
Je dôležité pochopiť pojem efektívnej úrokovej sadzby, pretože je životne dôležitou metrikou pre investora alebo iného finančného používateľa. Investori majú tendenciu využívať efektívnu úrokovú sadzbu predovšetkým preto, že je to skutočný výnos získaný z investície. Investori preto kladú väčší dôraz na počet kombinácií za rok, pretože vyšší počet kombinácií znamená vyšší výnos. Na druhej strane sa perspektíva mení pre dlžníka, ktorý sa usiluje o nižší počet kombinácií za rok, pretože by to udržiavalo nízke úrokové náklady a viedlo k lepšej ziskovosti.
Koncepcia efektívnej úrokovej sadzby veľmi závisí od toho, ako sa v priebehu roka dôjde k zloženiu, ktoré nakoniec zvýši výnos alebo prípadne vyššiu hodnotu spätného odkúpenia pri splatnosti. Efektívna ročná sadzba sa zvyčajne zvyšuje so zvyšujúcim sa počtom zložení za rok. Aj keď je zloženie možné vykonať nekonečne mnohokrát, je potrebné mať na pamäti, že existuje určitý limit na účinok zloženia a po uplynutí ktorého sa tento jav prestane vyskytovať. Tento typ zloženia je známy ako kontinuálne zloženie, pre ktoré je efektívna úroková miera vyjadrená ako - ei, i je uvedená úroková miera a je nezávislá od obdobia zloženia.
Efektívna kalkulačka úrokových mier
Môžete použiť nasledujúcu kalkulačku efektívnej úrokovej sadzby
| ja | |
| n | |
| Efektívna úroková sadzba | |
| Efektívna úroková sadzba | (1 + i / n) n -1 |
| = | (1 + 0/0) 0 -1 = 0 |
Odporúčané články
Toto je sprievodca vzorcom efektívnej úrokovej sadzby. Tu diskutujeme o výpočte efektívnej úrokovej sadzby spolu s praktickými príkladmi. Poskytujeme tiež kalkulačku efektívnej úrokovej sadzby so šablónou Excel na stiahnutie. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Vzorec pre mesačné zložené úroky
- Ako vypočítať nominálnu úrokovú sadzbu?
- Príklady úrokových nákladov
- Výpočet vzorca nominálneho HDP
- Úrok vs dividenda 8 najdôležitejších rozdielov, ktoré by ste mali vedieť