
Úvod do matematických funkcií v Pythone
V pythone sa všetky matematické potreby riešia pomocou pythonového matematického modulu. tento modul sa vyznačuje väčšinou klasifikáciou s rôznymi matematickými funkciami, ktoré sú do neho zabudované. Takmer všetky populárne matematické funkcie sú obsiahnuté v matematickom module. Toto je okamžite dostupný štandardný modul v pythone. Toto je možné importovať pomocou príkazu import math.
Rôzne matematické funkcie v Pythone
Všetky kľúčové matematické funkcie sú podrobne opísané nižšie,
1. Konštanty
V prípade matematickej konštanty je hodnota tejto konštanty reprezentovaná jednoznačnou definíciou, tieto definície sú v niektorých prípadoch reprezentované pomocou akýchkoľvek špeciálnych symbolov alebo známych mien matematikov alebo akýmkoľvek iným populárnym spôsobom. Konštanty sa vyskytujú v mnohých oblastiach matematiky pomocou konštánt ako π a e, ktoré sa dejú za rôznych okolností, ako je teória čísel, geometria a počet.
Význam konštanty, ktorá sa objaví „prirodzene“ a robí konštantnú „zaujímavú“, je v pravý čas nevyhnutný a množstvo matematických konštánt je výraznejších skôr z chronologických dôvodov, ako prostriedkami ich základného matematického záujmu. Najobľúbenejšie konštanty sa skúmali celé veky a počítali sa na veľa desatinných miest.
| konštanty | popis |
| pi | výnosy 3, 141592 |
| E | výnosy 0, 718282 |
| nan | Nie číslo |
| inf | nekonečný |
Príklad:
import math
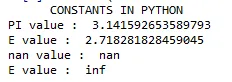
print( "CONSTANTS IN PYTHON")
print(" PI value : ", math.pi)
print(" E value : ", math.e)
print(" nan value : ", math.nan)
print(" E value : ", math.inf)
Výkon :
2. Logaritmické funkcie
Inverzia pre exponentiu sa nazýva logaritmus. Pre každé dané číslo x sa na určenie jeho príslušnej logaritmickej hodnoty vypočíta exponent iného pevného čísla so základňou b. V jednoduchšom prípade logaritmus vypočíta alebo spočíta číselné výskyty toho istého faktora pri opakovanom násobení;
Príklad: 1000 = 10 x 10 x 10 = 103, potom „logaritmus k báze 10“ 1000 je 3. Logaritmus x k báze b sa označuje ako logb (x).
Na druhej strane, exponent čísla znamená, koľkokrát je číslo použité v multiplikačnom faktore.
Príklad: 82 = 8 × 8 = 64
Slovami by sa reprezentácia 82 mohla nazývať „8 k mocnine 2“ alebo jednoducho ako „8 na druhú mocninu“ Na druhej strane, exponent čísla znamená, koľkokrát sa číslo použije v multiplikačnom faktore.
| funkcie | popis |
| exp (x) | Vráti e ** x |
| expm1 (x) | Vráti e ** x - 1 |
| log (x (, základ)) | x sa vráti do základnej logaritmy |
| log1p (x) | Vracia sa logaritmus hodnoty x1 základne |
| log2 (x) | Vracia sa logaritmus hodnoty x2 základne |
| log10 (x) | Vráti sa logaritmus hodnoty x10 bázy |
| pow (x, y) | Vráti x zdvihnutý na silu y |
| sqrt (x) | Vráti sa druhá odmocnina pre x |
Príklad:
import math
#variable declaration and assignation
Number_1 = 1
Number_2 = 2
Number_3 = 3
Number_4 = 4
# Applying exp() function
print(" EXPONENT VALUE ")
print(" Exponent value: ", math.exp(Number_1))
print(" \n ")
# Applying Base1 logarithm function
print(" BASE1 LOGARITHM " )
print(" BASE1 LOGARITHM VALUE of 2 : ", math.log1p(Number_2))
print(" \n " )
# Applying Base2 logarithm function
print(" BASE2 LOGARITHM " )
print(" BASE2 LOGARITHM VALUE of 2 : ", math.log2(Number_2))
print(" \n " )
# Applying Base10 logarithm function
print(" BASE10 LOGARITHM " )
print(" BASE10 LOGARITHM VALUE of 2 : ", math.log10(Number_2))
print(" \n " )
# Applying x to power of Y
print(" X^Y" )
print(" X^Y Value : ", math.pow(Number_3, Number_4))
print(" \n " )
# Applying square root determination
print(" SQUARE ROOT " )
print(" SQUARE ROOT of 4 : ", math.sqrt(Number_4))
print(" \n " )
Výkon :

3. Numerické funkcie
Numerické funkcie umožňujú výpočet všetkých matematických východísk.
| konštanty | popis |
| ceil (x) | Vráti sa najmenšie celé číslo, ktoré je oveľa väčšie alebo rovné hodnote x |
| copysign (x, y) | Pomocou znamienka y sa vráti hodnota pre x |
| FABS (X) | vráti sa absolútna hodnota pre x |
| faktoriálový (x) | vráti sa faktoriálna hodnota x |
| podlaha (x) | vráti sa najväčšie celé číslo, ktoré je oveľa menšie alebo rovné hodnote x |
| fmod (x, y) | vráti sa zvyšok delenia hodnoty x y |
| frexp (x) | Vráti mantisu a exponent x ako pár (m, e) |
| fsum (iterable) | Vráti presný súčet hodnôt s pohyblivou rádovou čiarkou v iterovateľnom poradí |
| isfinite (x) | ak x nie je nekonečno alebo Nan, boolovská hodnota true sa vráti |
| isinf (x) | ak x obsahuje kladnú alebo zápornú nekonečno, vráti sa true |
| isNaN (x) | Vráti true, ak x je NaN |
| gcd (x, y) | pre hodnotu xay sa vráti najbežnejšia spoločná hodnota deliteľa |
| zvyšok (x, y) | Nájdite zvyšok po delení x y. |
Príklad:
import math
#variable declaration and assignation
Number_1 = 10.5
Number_2 = 20
Number_3 = -30
Number_4 = -40.24566
Number_5 = 50
Number_6 = 60.94556
Number_7 = 70
Number_8 = 80
# Applying Ceil() function
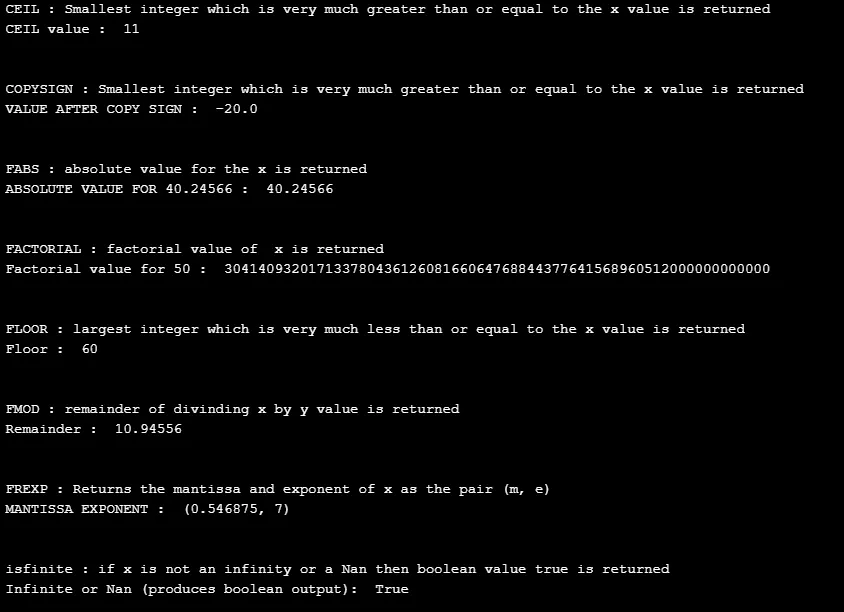
print( " CEIL : Smallest integer which is very much greater than or equal to the x value is returned ")
print( " CEIL value : ", math.ceil(Number_1))
print( " \n " )
# Applying Copysign() function
print( " COPYSIGN : Smallest integer which is very much greater than or equal to the x value is returned ")
Temp_var1 = math.copysign(Number_2, Number_3)
print(" VALUE AFTER COPY SIGN : ", Temp_var1)
print(" \n ")
# Applying fabs() function
print( " FABS : absolute value for the x is returned ")
print(" ABSOLUTE VALUE FOR 40.24566 : ", math.fabs(Number_4))
print(" \n ")
# Applying Factorial() function
print(" FACTORIAL : factorial value of x is returned ")
print(" Factorial value for 50 : ", math.factorial(Number_5))
print(" \n ")
# Applying Floor() function
print(" FLOOR : largest integer which is very much less than or equal to the x value is returned " )
print(" Floor : ", math.floor(Number_6))
print(" \n ")
# Applying Fmod() function
print(" FMOD : remainder of divinding x by y value is returned ")
print(" Remainder : ", math.fmod(Number_6, Number_5))
print(" \n ")
# Applying Frexp() function
print( " FREXP : Returns the mantissa and exponent of x as the pair (m, e) " )
print(" MANTISSA EXPONENT : ", math.frexp(Number_7))
print( " \n " )
# Applying isfinite() function
print(" isfinite : if x is not an infinity or a Nan then boolean value true is returned ")
print(" Infinite or Nan (produces boolean output): ", math.isfinite(Number_8))
print(" \n ")
Výkon:
4. Trigonometrické funkcie
V matematike sú trigonometrické funkcie funkcie, ktoré sa používajú na rozprávanie pohľadu na pravouhlý trojuholník v dvoch dĺžkach strán. majú veľmi rozsiahly súbor aplikácií vo vede, ktoré sú relatívne k geometrii, medzi ktoré patria mechanika pevných látok, nebeská mechanika, navigácia, mnoho ďalších. Tieto sa považujú za jednoduché periodické funkcie a všeobecne ich známe predstavujú periodické javy od začiatku do konca Fourierovej analýzy.
| funkcie | popis |
| sin (x) | Stanoví sa sínusová hodnota x v radiánoch |
| cos (x) | Je potrebné určiť kosínovú hodnotu x v radiánoch |
| tan (x) | musí sa určiť tangentná hodnota x v radiánoch |
| stupňov (X) | konverzia z radiánu na stupeň |
| radián (x) | konverzia stupňa na radián |
Príklad:
import math
print(" \n ")
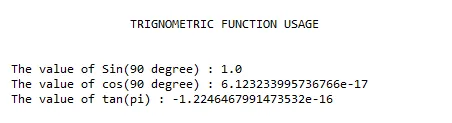
print(" TRIGNOMETRIC FUNCTION USAGE " )
print(" \n ")
print(' The value of Sin(90 degree) : ' + str(math.sin(math.radians(90))))
print(' The value of cos(90 degree) : ' + str(math.cos(math.radians(90))))
print(' The value of tan(pi) : ' + str(math.tan(math.pi)))
print(" \n ")
Výkon :
Záver - Matematické funkcie v Pythone
Rovnako ako mnoho iných programovacích jazykov, aj python ponúka veľmi rôznorodú množinu matematických funkcií, vďaka čomu je programovacím jazykom na vysokej úrovni v programovacej aréne.
Odporúčané články
Toto je sprievodca matematickými funkciami v Pythone. Tu uvádzame príklady rôznych matematických funkcií v Pythone. Môžete si tiež prečítať naše ďalšie navrhované články -
- Zoznam operácií v Pythone
- Factorial v Pythone
- String Array v Pythone
- Operácie so súbormi Python
- Matematické funkcie v C # s vlastnosťami
- Sady Pythonu
- Úvod do matematických funkcií v C
- Štvorcový koreň v PHP
- String Array v JavaScripte