
Úvod do DFS algoritmu
DFS je známy ako algoritmus hĺbkového prvého vyhľadávania, ktorý poskytuje kroky na prechádzanie každým uzlom grafu bez opakovania akéhokoľvek uzla. Tento algoritmus je pre strom rovnaký ako hĺbka prvého prechodu, ale pri udržiavaní booleovského jazyka sa líši v tom, či sa uzol už navštívil alebo nie. Toto je dôležité pre prechod grafom, pretože cykly tiež existujú v grafe. Zásobník je udržiavaný v tomto algoritme na ukladanie pozastavených uzlov počas prechodu. Nazýva sa to preto, že najprv prejdeme do hĺbky každého susediaceho uzla a potom pokračujeme v prechádzaní ďalším susediacim uzlom.
Vysvetlite algoritmus DFS
Tento algoritmus je v rozpore s algoritmom BFS, v ktorom sú navštívené všetky susedné uzly, za ktorými nasledujú susedia so susednými uzlami. Začne skúmať graf z jedného uzla a skúma jeho hĺbku pred spätným sledovaním. V tomto algoritme sa zvažujú dve veci:
- Návšteva vrcholu : Výber vrcholu alebo uzla grafu, ktorý sa má posúvať.
- Prieskum vrcholu : Prechádza všetkými uzlami susediacimi s týmto vrcholom.
Pseudo kód pre hĺbkové prvé vyhľadávanie :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Lineárny Traversal existuje aj pre DFS, ktorý môže byť implementovaný 3 spôsobmi:
- Predobjednať
- nevyhnutného
- postorder
Reverzná pošta je veľmi užitočný spôsob, ako prechádzať a používa sa pri topologickom triedení, ako aj pri rôznych analýzach. Zásobník sa tiež udržiava na uloženie uzlov, ktorých prieskum stále čaká.
Posúvanie grafov v DFS
V DFS sa nasledujúcimi krokmi postupuje grafom. Napríklad, daný graf, začnime prechodom od 1:
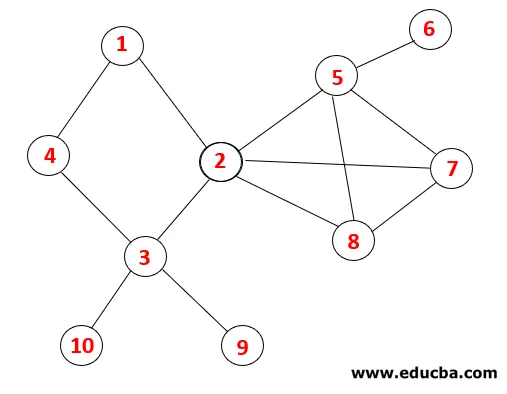
| Stoh | Traversal Sequence | Spanning Tree |
| 1 |  |
|
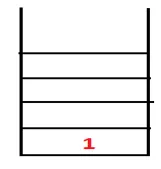 | 1, 4 |  |
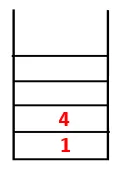 | 1, 4, 3 |  |
 | 1, 4, 3, 10 | 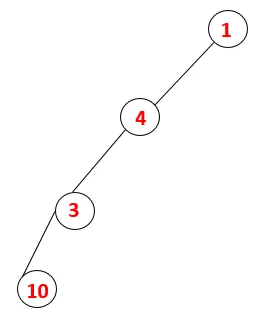 |
 | 1, 4, 3, 10, 9 | 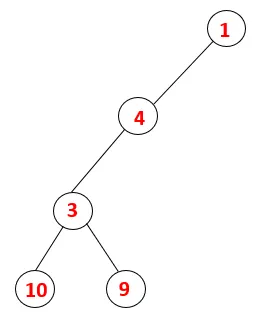 |
 | 1, 4, 3, 10, 9, 2 | 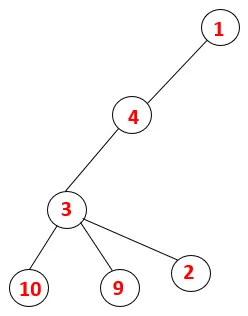 |
 | 1, 4, 3, 10, 9, 2, 8 |  |
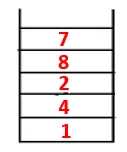
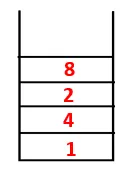 | 1, 4, 3, 10, 9, 2, 8, 7 | 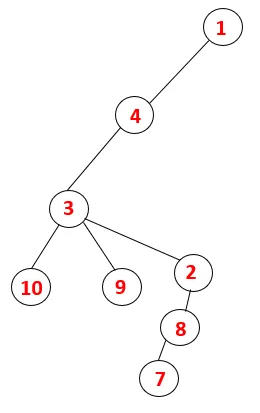 |
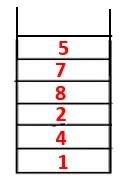
 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 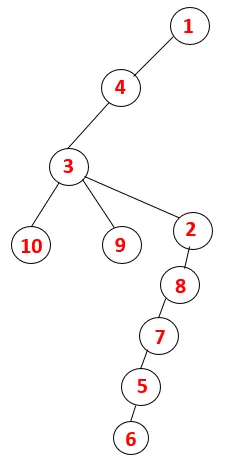 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 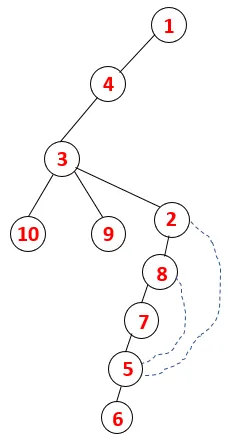 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
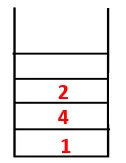 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 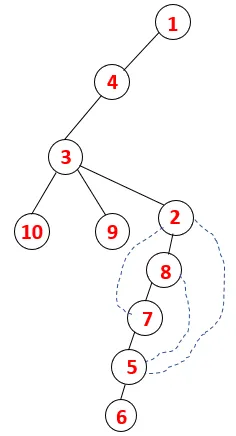 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 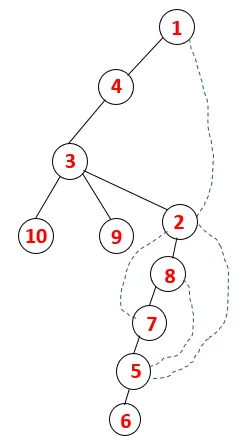 |
Vysvetlenie k algoritmu DFS
Nižšie sú uvedené kroky k algoritmu DFS s výhodami a nevýhodami:
Krok 1: Uzol 1 sa navštívi a pridá sa do sekvencie, ako aj do spanningového stromu.
Krok 2: Preskúmajú sa susedné uzly 1, ktoré sú 4, takže 1 je poslaný do stohu a 4 je zasunutý do sekvencie, ako aj do preklenovacieho stromu.
Krok 3: Preskúma sa jeden zo susedných uzlov 4, a tak sa 4 posúva do stohu a 3 vstupuje do postupnosti a preklenovacieho stromu.
Krok 4: Susedné uzly 3 sú preskúmané ich zatlačením na stoh a 10 vstupuje do sekvencie. Pretože neexistuje žiadny susedný uzol k 10, tak sa 3 vyskočí zo stohu.
Krok 5: Preskúma sa ďalší susedný uzol 3 a 3 sa zatlačí na stoh a navštívi sa 9. Žiadny susedný uzol 9, teda 3, nie je vysunutý a je navštívený posledný susedný uzol 3, tj 2.
Podobný proces sa uplatňuje pre všetky uzly, až kým sa zásobník nevyprázdni, čo indikuje stav zastavenia pre algoritmus prechodu. - -> prerušované čiary v preklenovacom strome znamenajú zadné okraje prítomné v grafe.
Týmto spôsobom sa všetky uzly v grafe posúvajú bez opakovania ktoréhokoľvek z uzlov.
Výhody a nevýhody
- Výhody: Tieto požiadavky na pamäť pre tento algoritmus sú veľmi menšie. Menšia zložitosť priestoru a času ako BFS.
- Nevýhody: Riešenie nie je zaručené Aplikácie. Topologické triedenie. Hľadanie mostov grafu.
Príklad implementácie algoritmu DFS
Nižšie je uvedený príklad implementácie algoritmu DFS:
kód:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Výkon:
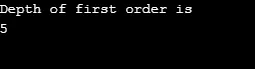
Vysvetlenie k vyššie uvedenému programu: Vytvorili sme graf s 5 vrcholmi (0, 1, 2, 3, 4) a použili sme navštívené pole na sledovanie všetkých navštívených vrcholov. Potom pre každý uzol, ktorého susedné uzly existujú, sa ten istý algoritmus opakuje, až kým sa nenavštívia všetky uzly. Potom sa algoritmus vráti na volanie vrcholu a vyskočí zo zásobníka.
záver
Pamäťová náročnosť tohto grafu je v porovnaní s BFS menšia, pretože je potrebné udržiavať iba jeden zväzok. Výsledkom je vygenerovaný preklenovací strom DFS a postupnosť, ktorá nie je konštantná. Je možné viacnásobné posúvanie v závislosti od začiatočného vrcholu a vybraného vrcholu prieskumu.
Odporúčané články
Toto je sprievodca algoritmom DFS. Tu diskutujeme o postupnom vysvetľovaní, prechádzame grafom v tabuľkovom formáte s výhodami a nevýhodami. Viac informácií nájdete aj v ďalších súvisiacich článkoch -
- Čo je to HDFS?
- Algoritmy hlbokého učenia
- Príkazy HDFS
- Algoritmus SHA