
Vzorec štatistickej skúšky Z (obsah)
- vzorec
- Príklady
- kalkulačka
Čo je to štatistický vzorec testu Z?
Z Štatistika testu je štatistický postup používaný na testovanie alternatívnej hypotézy proti nulovej hypotéze. Je to akákoľvek štatistická hypotéza použitá na určenie, či sa dva spôsoby vzoriek líšia, keď sú známe odchýlky a vzorka je veľká. Z Test určuje, či existuje významný rozdiel medzi prostriedkami vzorky a populácie. Z Test bežne používaný na riešenie problémov týkajúcich sa veľkých vzoriek. Názov jednotky „z test“ z tejto interferencie sa vyrába zo štandardnej normálnej distribúcie a „Z“ je tradičný symbol používaný na označenie štandardnej normálnej náhodnej premennej. Testovací vzorec Z vypočítaný vzorkou znamená mínus počet obyvateľov vydelený štandardnou odchýlkou populácie a veľkosťou vzorky. Ak je veľkosť vzorky viac ako 30 jednotiek ako v takom prípade, musí sa vykonať test z. Matematicky z testovací vzorec je vyjadrený ako,
Z Test = (x̄ – μ) / ( σ / √n)
Tu,
- x̄ = priemer vzorky
- μ = Priemerný počet obyvateľov
- σ = smerodajná odchýlka obyvateľstva
- n = počet pozorovaní
Príklady vzorcov štatistických testov Z (so šablónou programu Excel)
Pozrime sa na lepšie pochopenie výpočtu vzorca Z Test Statistics.
Túto šablónu Z Test Statistics Formula Formula Excel si môžete stiahnuť tu - Z Test Statistics Formula Formula Excel TemplateVzorec štatistík testu Z - príklad č. 1
Predpokladajme, že niekto chce skontrolovať alebo otestovať, či čaj a káva sú v meste rovnako populárne. V takom prípade môže použiť štatistickú metódu az testov na získanie výsledkov tým, že odoberie vzorku s veľkosťou 500 z mesta, z ktorých sa predpokladá, že pijú čaj 280. Na testovanie tejto hypotézy môže použiť testovaciu metódu z.
Riaditeľ školy tvrdí, že študenti jeho školy majú nadpriemernú inteligenciu a náhodná vzorka 30 študentov IQ skóre má priemerné skóre 112, 5 a priemerný IQ populácie je 100 so štandardnou odchýlkou 15. Existuje dostatok dôkazov na podporu hlavného tvrdenia ?
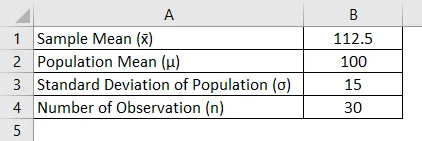
Riešenie:
Z Štatistika testu sa vypočíta pomocou vzorca uvedeného nižšie
Z test = (x̄ - μ) / ( σ / √n)
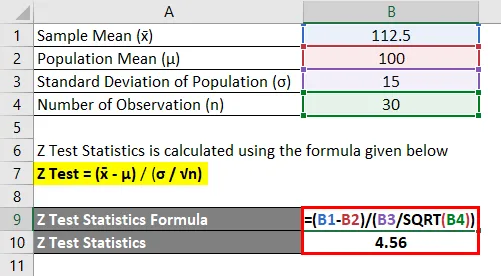
- Z test = (112, 5 - 100) / (15/30)
- Z test = 4, 56
Porovnajte výsledky z testu so štandardnou tabuľkou z testu a v tomto príklade môžete dospieť k záveru, že nulová hypotéza je zamietnutá a hlavný nárok je správny.
Vzorec štatistík testu Z - príklad č. 2
Predpokladajme, že investor, ktorý chce analyzovať priemerný denný výnos akcií jednej spoločnosti, je väčší ako 1% alebo nie? Investori teda vybrali náhodnú vzorku 50 a vypočítal sa výnos, ktorý má priemer 0, 02 a investori považujú štandardnú odchýlku priemeru za 0, 025.
V tomto prípade je nulová hypotéza vtedy, keď je priemer 3% a alternatívna hypotéza je, že priemerný výnos je vyšší ako 3%. Investori predpokladajú, že alfa 0, 05% je vybraný ako dvojstranný test a 0, 025% vzorky v každom chvoste a kritická hodnota alfa je 1, 96 alebo -1, 96. Ak je teda výsledok testu Z menší alebo väčší ako 1, 96, neplatná hypotéza bude zamietnutá.
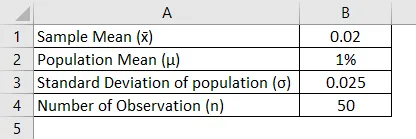
Riešenie:
Z Štatistika testu sa vypočíta pomocou vzorca uvedeného nižšie
Z test = (x̄ - μ) / ( σ / √n)
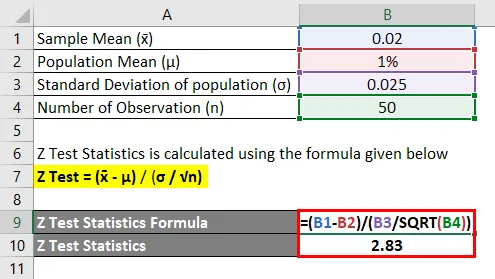
- Z test = (0, 02 - 1%) / (0, 025 / ~ 50)
- Z test = 2, 83
Z vyššie uvedeného výpočtu teda investori dospejú k záveru a odmietne nulovú hypotézu, pretože výsledok z je väčší ako 1, 96 a dospeje k analýze, že priemerný denný výnos akcie je vyšší ako 1%.
Vzorec štatistík testu Z - príklad č. 3
Poisťovňa v súčasnosti prehodnocuje svoje súčasné poistné sadzby, keď pôvodne nastavila mieru, o ktorej sa domnievajú, že priemerná výška poistnej udalosti bude maximálne 18 000 Rs. Spoločnosť sa obáva, že tento skutočný priemer je skutočne vyšší ako tento. Spoločnosť náhodne vyberie 40 vzorových nárokov a vypočíta strednú hodnotu vzorky Rs 195000 za predpokladu, že štandardná odchýlka nároku je R 50000 a nastaví sa alfa ako 0, 05. Takže test z, ktorý sa má vykonať, aby ste videli poisťovňu, by sa mal týkať alebo nie.
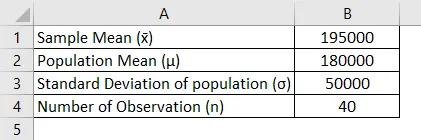
Riešenie:
Z Štatistika testu sa vypočíta pomocou vzorca uvedeného nižšie
Z test = (x̄ - μ) / ( σ / √n)
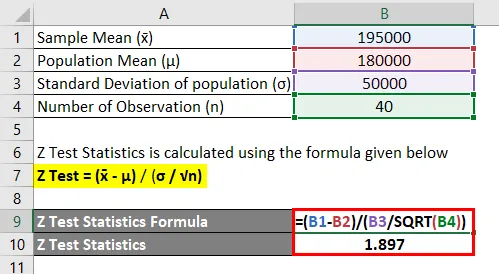
- Z test = (195000 - 180000) / (50000 / -40)
- Z test = 1, 897
Krok - 1 Nastavte nulovú hypotézu
Krok - 2 vypočíta štatistiku testu
Takže ak dáte všetky dostupné čísla do vzorcov z testu, dá nám výsledky z výsledkov z 1.897
Krok - 3 Nastavte oblasť odmietnutia
Ak vezmeme do úvahy alfa ako 0, 05, povedzme, oblasť odmietnutia je 1, 65
Krok - 4 Záver
Pokiaľ ide o výsledky testu z, vidíme, že 1, 897 je väčšia ako oblasť odmietnutia 1, 65, takže spoločnosť neakceptuje nulovú hypotézu a poisťovňa by sa mala zaoberať ich súčasnými poistnými zmluvami.
vysvetlenie
- Najprv stanovte priemer vzorky (je to vážený priemer všetkých náhodných vzoriek).
- Stanovte priemerný priemer populácie a odčítajte od nej priemerný priemer vzorky.
- Potom vydeľte výslednú hodnotu štandardnou odchýlkou vydelenou druhou odmocninou viacerých pozorovaní.
- Po vykonaní vyššie uvedených krokov sa vypočítajú výsledky testov.
Relevantnosť a použitie štatistického vzorca pre skúšky Z
Z test sa používa na porovnanie priemeru normálnej náhodnej premennej so špecifikovanou hodnotou. Test Z je užitočný alebo sa má použiť, ak je vzorka vyššia ako 30 a je známa odchýlka populácie. Test Z je najlepší za predpokladu, že stredná hodnota distribúcie vzorky je normálna. Test Z sa použije, ak sú stanovené určité podmienky, inak je potrebné použiť iné testy a pri teste z neexistujú fluktuácie. Z test pre jeden prostriedok sa používa na testovanie hypotézy špecifickej hodnoty priemeru populácie. Test Z je jednou zo základných metód testovania štatistických hypotéz a často sa učí na úvodnej úrovni. Ak sa údaje generujú z inej distribúcie, napríklad z binomického a Poissonovho indexu, je možné použiť testy času z.
Z Kalkulačka vzorcov štatistík testov
Môžete použiť nasledujúcu kalkulačku štatistík testu Z
| X | |
| μ | |
| σ | |
| √n | |
| Z Test | |
| Z Test = |
|
|
Odporúčané články
Toto bol sprievodca Z Test Statistics Formula. Tu diskutujeme o tom, ako vypočítať štatistiku testu Z spolu s praktickými príkladmi. Poskytujeme tiež kalkulačku štatistík testu Z so šablónou Excel na stiahnutie. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Čo je to hypergeometrický distribučný vzorec?
- Vzorec na testovanie hypotéz Definícia kalkulačka
- Príklady koeficientu stanovenia
- Ako vypočítať veľkosť vzorky pomocou vzorca?