
Úvod k príkladom štandardnej odchýlky
Existuje dostatok príkladov štandardných odchýlok. Štandardná odchýlka je miera rozptylu množiny údajov, tj miera rozloženia čísel. Je to užitočné pri porovnávaní rôznych súborov údajov, ktoré môžu mať rovnaký priemer, ale odlišný rozsah. Nasledujúci iný príklad smerodajnej odchýlky poskytuje pochopenie najbežnejších typov situácií, v ktorých sa štandardná odchýlka počíta, a ako je možné vypočítať tú istú hodnotu.
Príklady štandardnej odchýlky
Ďalej uvádzame príklady smerodajnej odchýlky
Štandardná odchýlka - príklad č. 1
Akciová spoločnosť Z predáva za 50 dolárov za akciu a rovnaké ponuky ponúka nasledujúce výplaty pre nasledujúci rok:
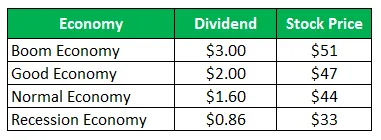
Vypočítajte smerodajnú odchýlku, keď sú všetky štyri scenáre rovnako pravdepodobné.
Riešenie:
Výpočty návratnosti obdobia držby (HPR) sú nasledujúce -
Vzorec HPR
HPR = ((hodnota na konci obdobia - pôvodná hodnota) + príjem) / pôvodná hodnota) * 100
Pre ekonomiku boomu
- HPR (Boom) = ((51-50) + 3) / 50 = 8, 00%
- HPR (dobrý) = ((47-50) + 2) / 50 = -2, 00%
- HPR (normálne) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (Recesia) = ((33-50) + 0, 86) / 50 = -32, 28%
Výpočet očakávaného výnosu
Keďže všetky scenáre sú rovnako pravdepodobné, pravdepodobnosť všetkých bude ¼
Vzorec očakávaného návratu
Očakávaný výnos = (Pravdepodobnosť rozmachu * Návrat z rozmachu) + (Pravdepodobnosť dobra * Návrat z dobra) + (Pravdepodobnosť normálu * Návrat z normálu) + (Pravdepodobnosť recesie * Návrat z recesie)
- Očakávaný výnos = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Očakávaný výnos = -8, 77%
Výpočet smerodajnej odchýlky
Vzorec variancie
Variant = (Pravdepodobnosť rozmachu * (Návrat z rozmachu - celkový očakávaný výnos) 2) + (Pravdepodobnosť dobrého * (návratnosť z dobrého - celkový očakávaný výnos) 2) + (Pravdepodobnosť normálu * (Návrat z normálu - celkový očakávaný výnos) 2 ) + (Pravdepodobnosť recesie * (návrat z recesie - celkový očakávaný návrat) 2)
- Varianta = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Varianta = 219, 95
Vzorec štandardnej odchýlky
Štandardná odchýlka bude druhá odmocnina
Štandardná odchýlka = arVelivosť
- Štandardná odchýlka = √ 219, 95
- Štandardná odchýlka = 14, 83%
Príklad štandardnej odchýlky - 2
Štandardná odchýlka v prípade dvoch spoločností v portfóliu
Kmeňové akcie spoločnosti A predávajú za 28 dolárov na akciu a rovnaké ponuky po výplatách na budúci rok

Kmeňové akcie spoločnosti B predávajú za 93 dolárov za akciu a rovnaké ponuky ponúkajú nasledujúce výplaty za budúci rok:

(a) Vypočítajte štandardnú odchýlku spoločnosti A
(b) Vypočítajte štandardnú odchýlku spoločnosti B
(c) Vypočítajte štandardnú odchýlku portfólia, ak sa uskutoční polovica investície, a to spoločnosť A a polovica zvyšku v spoločnosti B
Riešenie:
Pre spoločnosť A
Výpočty návratnosti obdobia držby (HPR)
Vzorec HPR
HPR = ((hodnota na konci obdobia - pôvodná hodnota) + príjem) / pôvodná hodnota) * 100
- HPR (boom) = ((20-28) + 1) / 28 = -25, 00%
- HPR (normálne) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (Recesia) = ((38-28) + 5) / 28 = 53, 57%
Výpočet očakávaného návratu spoločnosti A
Vzorec očakávaného návratu
Očakávaný výnos = (pravdepodobnosť rozmachu * návrat z rozmachu) + (pravdepodobnosť normálu * návrat z normálu) + (pravdepodobnosť recesie * návrat z recesie)
- Očakávaný výnos = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Očakávaný výnos = 3, 84%
Výpočet spoločnosti so štandardnou odchýlkou A
Vzorec variancie
Variant = (Pravdepodobnosť rozmachu * (návrat z rozmachu - celkový očakávaný výnos) 2) + (pravdepodobnosť normálu * (návratnosť z normálu - celkový očakávaný výnos) 2 ) + (pravdepodobnosť recesie * (návrat z recesie - celkový očakávaný výnos)) 2)
- Varianta = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Varianta = 895, 15
Vzorec štandardnej odchýlky
Štandardná odchýlka bude druhá odmocnina
Štandardná odchýlka = arVelivosť
- Štandardná odchýlka = √ 895, 15
- Štandardná odchýlka = 29, 92%
Pre spoločnosť B
Výpočty návratnosti obdobia držby (HPR)
Vzorec HPR
HPR = ((hodnota na konci obdobia - pôvodná hodnota) + príjem) / pôvodná hodnota) * 100
HPR (Boom) = ((200-93) +7) / 93 = 122, 58%
HPR (normálne) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (Recesia) = ((4-93) +2) / 93 = -93, 55%
Výpočet očakávaného výnosu
Vzorec očakávaného návratu
Očakávaný výnos = (pravdepodobnosť rozmachu * návrat z rozmachu) + (pravdepodobnosť normálu * návrat z normálu) + (pravdepodobnosť recesie * návrat z recesie)
- Očakávaný výnos = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Očakávaný výnos = 43, 04%
Výpočet smerodajnej odchýlky
Vzorec variancie
Variant = (Pravdepodobnosť rozmachu * (návrat z rozmachu - celkový očakávaný výnos) 2) + (pravdepodobnosť normálu * (návratnosť z normálu - celkový očakávaný výnos) 2 ) + (pravdepodobnosť recesie * (návrat z recesie - celkový očakávaný výnos)) 2)
- Variácia = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Varianta = 6783, 65
Vzorec štandardnej odchýlky
Štandardná odchýlka bude druhá odmocnina
Štandardná odchýlka = arVelivosť
- Štandardná odchýlka = 6783, 65
- Štandardná odchýlka = 82, 36%
Výpočet očakávaného výnosu a štandardnej odchýlky portfóliovej polovice investovanej do spoločnosti A a polovice do spoločnosti B.
Štandardná odchýlka spoločnosti A = 29, 92%
Štandardná odchýlka spoločnosti B = 82, 36%
Hmotnosť spoločnosti A = 0, 50
Hmotnosť spoločnosti B = 0, 50
Vzorec Štandardná odchýlka portfólia
Štandardná odchýlka portfólia = (váha spoločnosti A * očakávaná návratnosť spoločnosti A) + ((váha spoločnosti B * očakávaná návratnosť spoločnosti B)
- Štandardná odchýlka portfólia = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Štandardná odchýlka portfólia = 56, 14%
analýza
Štandardná štandardná odchýlka portfólia je nižšia ako v prípade jednotlivcov jednotlivých akcií, pretože akcie sú diverzifikované do rôznych akcií. Diverzifikácia vedie k zníženiu rizika, pokiaľ medzi výnosmi z portfóliových investícií neexistuje korelácia.
Záver - príklady štandardnej odchýlky
Štandardná odchýlka meria rozptyl súboru údajov, ktorý je relatívny k jeho priemeru. Vypočíta sa ako druhá odmocnina rozptylu. Čím väčšia je štandardná odchýlka cenného papiera, tým väčší bude rozdiel medzi každou cenou a priemerom, čo ukazuje, že cenové rozpätie je veľké. Vyššie uvedené príklady sú niektoré z príkladov smerodajnej odchýlky rôznymi spôsobmi. Existujú aj rôzne ďalšie príklady, ktoré ukazujú, že smerodajná odchýlka sa môže vypočítať pomocou iných údajov.
Odporúčané články
Toto bol sprievodca štandardnými príkladmi odchýlok. Tu diskutujeme rôzne príklady štandardnej odchýlky spolu s podrobným vysvetlením . Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Príklad fixných nákladov
- Príklad variabilnej kalkulácie
- Príklad kvantitatívneho výskumu
- Príklady monopolistickej hospodárskej súťaže