Úvod do hierarchického klastrovacieho algoritmu
Hierarchický klastrovací algoritmus je technika strojového učenia bez dozoru. Jeho cieľom je nájsť prirodzené zoskupenie na základe charakteristík údajov.
Hierarchický klastrovací algoritmus má za cieľ nájsť vnorené skupiny údajov vytvorením hierarchie. Je to podobné biologickej taxonómii rastlinnej alebo živočíšnej ríše. Hierarchické klastre sa všeobecne reprezentujú pomocou hierarchického stromu známeho ako dendrogram.
Druhy hierarchického klastrovacieho algoritmu
Hierarchické klastrové algoritmy sú 2 typov:
- rozvratný
- aglomerativní
1. Rozdeľujúce
Jedná sa o prístup zhora nadol, kde spočiatku považuje celé údaje za jednu skupinu a potom iteratívne rozdelí údaje do podskupín. Ak je známy počet hierarchických klastrových algoritmov, proces rozdelenia sa zastaví, keď sa dosiahne počet klastrov. V opačnom prípade sa proces zastaví, keď už nie je možné údaje rozdeliť, čo znamená, že podskupina získaná z aktuálnej iterácie je rovnaká ako tá, ktorá bola získaná z predchádzajúcej iterácie (je možné tiež zvážiť, že delenie sa zastaví, keď je každý dátový bod zhlukom). ).
2. Aglomerát
Je to prístup zdola nahor, ktorý sa opiera o zlúčenie zoskupení. Na začiatku sú dáta rozdelené do m singletónových zhlukov (kde hodnota m je počet vzoriek / dátových bodov). Dva klastre sa zlúčia do jednej iteratívne, čím sa zníži počet klastrov v každej iterácii. Tento proces zlúčenia klastrov sa zastaví, keď sa všetky klastre zlúčia do jedného alebo sa dosiahne požadovaný počet klastrov.
Na úrovni 1 sú klastre m, ktoré sa redukujú na 1 klaster na úrovni m. Tie dátové body, ktoré sa zlúčia a vytvoria klaster na nižšej úrovni, zostanú v rovnakom klastri aj na vyšších úrovniach. Predpokladajme napríklad, že existuje 8 bodov x1..x8, takže spočiatku existuje 8 klastrov na úrovni 1. Predpokladajme, že body x1 a x2 sa zlúčia do klastra na úrovni 2, potom až do úrovne 8, zostanú v rovnakom klastri.
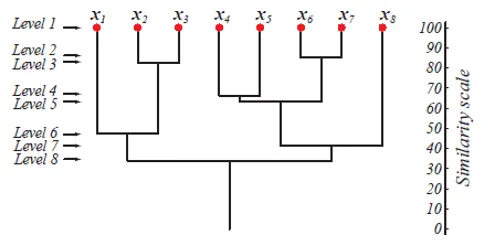
Vyššie uvedený obrázok ukazuje dendrogramové znázornenie aglomeračného prístupu klastrovania pre 8 dátových bodov, ako aj stupnicu podobnosti zodpovedajúcu každej úrovni.
Úrovne zhlukov nám poskytujú predstavu o tom, aké podobné sú dátové body v zhlukoch. Ako je znázornené na obr. 1, čím skôr sa dátové body zlúčia do klastra, sú podobné. Takže dátové body v klastri na úrovni 2 (napr. X2 a x3) sú podobnejšie ako tie dátové body v klastri na úrovni 6 (napr. X1 a x2).
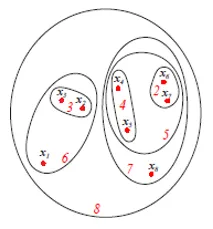
Horeuvedený obrázok predstavuje zobrazenie diagramu Set alebo Venn aglomeračného zoskupovania vyššie uvedených 8 dátových bodov. Na zoskupovanie sa môžu použiť dendrogramy aj reprezentácie množín. Avšak dendrogram je zvyčajne výhodný reprezentácia majetku, ktorý nemôže kvantitatívne reprezentovať podobnosti klastrov.
Kroky pre hierarchický klastrovací algoritmus
Postupujeme podľa nasledujúcich krokov pre algoritmus hierarchického zoskupovania, ktorý je uvedený nižšie:
1. Algoritmus
Aglomeračný hierarchický klastrovací algoritmus
- Začnite inicializáciu c, c1 = n, Di = (xi), i = 1, …, n '
- Do c1 = c1 - 1
- Nájdite najbližšie klastre, povedzme, Di a Dj
- Zlúčiť Di a Dj
- Kým c = c1
- Návrat klastrov c
- Koniec
Tento algoritmus začína na začiatku n klastrov, kde každý dátový bod je klaster. S každou iteráciou sa počet klastrov zníži o 1, keď sa zlúčia 2 najbližšie klastre. Tento proces pokračuje, kým sa počet klastrov nezníži na vopred definovanú hodnotu c.
Ako sa rozhodnúť, ktoré zoskupenia sú najbližšie?
Definuje sa pomocou niekoľkých metrík vzdialenosti, ktoré sú nasledujúce:
- Minimálna vzdialenosť medzi klastrami dmin (Di, Dj). Užitočné pre jedného.
- Maximálna vzdialenosť medzi klastrami dmax (Di, Dj). Užitočné pre dokončenie.
- Priemerná vzdialenosť medzi klastrami davg (Di, Dj).
Čo je to Single Linkage a Complete Linkage?
- Ak sa na nájdenie vzdialenosti medzi dvoma klastrami použije dmin (di, dj) a algoritmus sa ukončí, ak vzdialenosť medzi najbližšími klastrami prekročí prahovú hodnotu, potom sa tento algoritmus nazýva algoritmus jednoduchej väzby.
- Keď sa použije dmax (Di, Dj) na nájdenie vzdialenosti medzi dvoma klastrami a algoritmus sa ukončí, ak vzdialenosť medzi najbližšími klastrami prekročí prahovú hodnotu, potom sa algoritmus nazýva algoritmus úplného prepojenia.
- Uvažujme každý údajový bod ako uzol grafu. Medzi dvoma dátovými bodmi je hrana, ak patria do toho istého klastra. Keď sa zlúčia dva najbližšie klastre, pridá sa okraj. Nazýva sa to jediné spojenie, pretože existuje jedinečná cesta z jedného uzla na druhý.
- Algoritmus úplného prepojenia spája dva zoskupenia minimalizovaním vzdialenosti medzi dvoma najvzdialenejšími bodmi.
- Jeden algoritmus prepojenia generuje preklenovací strom. Tento algoritmus je však citlivý na šum. Algoritmus úplného prepojenia generuje kompletný graf.
Aká je časová zložitosť algoritmu?
Predpokladajme, že máme n obrazcov v d-dimenzionálnom priestore a na vytvorenie klastrov c použijeme dmin (Di, Dj). Potrebujeme vypočítať n (n - 1) medzistupňové vzdialenosti - každá z nich je výpočtom O (d 2 ) - a výsledky umiestniť do tabuľky medzibodových vzdialeností. Priestorová zložitosť je O (n 2 ). Nájdenie páru minimálnej vzdialenosti (pre prvé zlúčenie) si vyžaduje, aby sme prešli kompletným zoznamom a udržali index najmenšej vzdialenosti.
Takže pre prvý aglomeračný krok je komplexnosť O (n (n - 1) (d2 + 1)) = 0 (n2d2). Pre ďalší ľubovoľný krok aglomerácie (tj od c1 do c1 - 1) iba prechádzame n (n - 1) - c1 „nepoužitými“ vzdialenosťami v zozname a nájdeme najmenšiu, pre ktorú sú x a x 'v rôznych zoskupeniach, Toto je opäť O (n (n-1) -c1). Celková časová zložitosť je teda O (cn 2 d2) a za typických podmienok n >> c.
2. Vizualizácia
Keď sa údaje rozdelia do zoskupení, je dobré si zoskupenia zoskupiť, aby ste získali predstavu o tom, ako vyzerá zoskupenie. Vizualizácia týchto vysokorozmerných údajov je však zložitá. Preto na vizualizáciu používame analýzu hlavných komponentov (PCA). Po PCA získame dátové body v nízkorozmernom priestore (zvyčajne 2D alebo 3D), ktoré môžeme vykresliť, aby sme videli zoskupenie.
Poznámka: Vysoký rozmer znamená veľký počet funkcií a nie počet údajových bodov.3. Hodnotenie
Jednou z metód na hodnotenie klastrov je to, že vzdialenosť bodov medzi klastrami (vzdialenosť medzi klastrami) by mala byť oveľa väčšia ako vzdialenosť bodov v rámci klastrov (vzdialenosť medzi klastrami).
záver
Nasleduje niekoľko dôležitých krokov:
- Hierarchický klastrovací algoritmus sa používa na nájdenie vnorených vzorov v údajoch
- Hierarchické zoskupovanie je 2 typov - Divisive a Agglomerative
- Na znázornenie možno použiť dendrogram a schému / Venn diagram
- Jediné prepojenie spája dva zoskupenia minimalizovaním minimálnej vzdialenosti medzi nimi. Tvorí to preklenutie
- Kompletné prepojenie spája dva zoskupenia minimalizovaním maximálnej vzdialenosti medzi tým, že vytvára kompletný graf.
- Celková časová zložitosť hierarchického klastrovacieho algoritmu je O (cn 2 d 2 ), kde c je preddefinovaný počet zhlukov, n je počet vzorov a d je d-rozmerný priestor n obrazcov.
Odporúčané články
Toto je príručka k algoritmu hierarchického zoskupovania. Tu diskutujeme typy a kroky hierarchických klastrových algoritmov. Viac informácií nájdete aj v nasledujúcich článkoch
- Hierarchická klastrová analýza
- Hierarchické zhlukovanie v R '
- Clustering Algorithm
- Čo je klastrovanie v ťažbe údajov?
- Hierarchické zoskupovanie Aglomeračné a deliace sa zoskupovanie
- Algoritmus C ++ Príklady algoritmu C ++