Úvod do hierarchického klastra
- Jeden z našich klientov nedávno požiadal náš tím, aby priniesol zoznam segmentov s poradím dôležitosti v rámci svojich zákazníkov, aby ich zamerali na franšízu jedného zo svojich novo zavedených produktov. Je zrejmé, že iba segmentácia zákazníkov pomocou čiastočného zoskupovania (k-znamená, c-fuzzy) neprinesie poradie dôležitosti, z čoho vyplýva hierarchické zoskupovanie.
- Hierarchické zoskupovanie delí údaje do rôznych skupín na základe niektorých opatrení podobnosti známych ako zoskupenia, ktoré sa v zásade zameriavajú na vytváranie hierarchie medzi zoskupeniami. Je to v podstate učenie bez dozoru a výber atribútov na meranie podobnosti je špecifický pre konkrétnu aplikáciu.
Hierarchia klastrov údajov
- Aglomeračné zhlukovanie
- Divisive Clustering
Zoberme si príklad údajov, známok získaných od 5 študentov, ktoré ich zoskupia do pripravovanej súťaže.
| študent | marks |
| 10 | |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Aglomeračné zhlukovanie
- Najprv považujeme každý jednotlivý bod / prvok za dôležitý ako klastre a pokračujeme v spájaní podobných bodov / prvkov do nového klastra na novej úrovni, až kým nezostaneme pri jedinom klastri, je prístup zdola nahor.
- Jediné spojenie a úplné spojenie sú dva populárne príklady aglomeračného zoskupovania. Iné ako priemerné a stredové spojenie. V jednom prepojení zlúčime v každom kroku dva zoskupenia, ktorých dvaja najbližší členovia majú najmenšiu vzdialenosť. Pri úplnom prepojení sa spojíme s členmi najmenšej vzdialenosti, ktoré poskytujú najmenšiu maximálnu vzdialenosť v pároch.
- Matica blízkosti, je to jadro pre vykonávanie hierarchického zoskupovania, ktoré dáva vzdialenosť medzi jednotlivými bodmi.
- Vytvorme si proximitnú maticu pre naše údaje uvedené v tabuľke, pretože vypočítame vzdialenosť medzi každým z bodov s ostatnými bodmi, bude to asymetrická matica tvaru n × n, v našom prípade 5 × 5 matíc.
Populárna metóda pre výpočet vzdialenosti je:
- Euklidovská vzdialenosť (druhá mocnina)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Manhattanská vzdialenosť
dist((x, y), (a, b)) =|x−c|+|y−d|
Euklidovská vzdialenosť sa najčastejšie používa, budeme ju používať rovnako a pôjdeme so zložitým prepojením.
| Študent (zoskupenia) | B | C | D | E | |
| 0 | 3 | 18 | 10 | 25 | |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Diagonálne prvky proximitnej matice budú vždy 0, pretože vzdialenosť medzi bodom s rovnakým bodom bude vždy 0, preto sú diagonálne prvky vylúčené zo zvažovania pri zoskupovaní.
V iterácii 1 je najmenšia vzdialenosť 3, preto zlúčime A a B a vytvoríme zhluk, opäť vytvoríme novú proximitnú maticu s zhlukom (A, B), pričom (A, B) zhluk získame ako 10, tj maximum ( 7, 10) tak by bola novo vytvorená proximitná matica
| klastre | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
V iterácii 2, 7 je minimálna vzdialenosť, preto zlúčime C a E a vytvoríme nový klaster (C, E), opakujeme proces, ktorý sme opakovali v iterácii 1, až kým neskončíme s jediným klastrom, tu zastavíme pri iterácii 4.
Celý proces je znázornený na nasledujúcom obrázku:
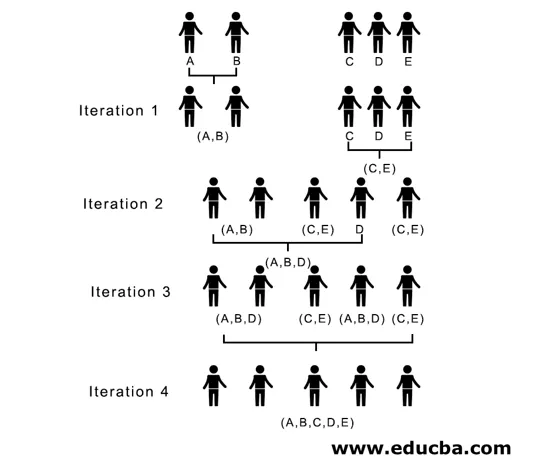
(A, B, D) a (D, E) sú 2 zoskupenia vytvorené pri iterácii 3, pri poslednej iterácii vidíme, že nám zostáva jeden klaster.
2. Delenie zhlukov
Na začiatok považujeme všetky body za jeden klaster a oddeľujeme ich najvzdialenejšou vzdialenosťou, kým neskončíme jednotlivými bodmi ako jednotlivé klastre (nie nevyhnutne môžeme zastaviť v strede, záleží na minimálnom počte prvkov, ktoré chceme v každom klastri) v každom kroku. Je to pravý opak aglomeračného zoskupovania a je to prístup zhora nadol. Deliace sa zhlukovanie je spôsob, ako sa opakujúce sa k znamená zhlukovanie.
Výber medzi aglomeračným a deliacim sa zhlukom je opäť závislý od aplikácie, napriek tomu je potrebné zvážiť niekoľko bodov:
- Delenie je zložitejšie ako aglomeračné zoskupovanie.
- Rozdeľovacie zoskupovanie je efektívnejšie, ak negenerujeme úplnú hierarchiu až po jednotlivé dátové body.
- Aglomeračné zoskupovanie sa rozhoduje na základe zváženia miestnych problémov, pričom pôvodne sa nezohľadňujú globálne vzorce, ktoré nemožno zvrátiť.
Vizualizácia hierarchického klastra
Veľmi užitočnou metódou vizualizácie hierarchického zoskupovania, ktorá pomáha v podnikaní, je Dendogram. Dendogramy sú stromové štruktúry, ktoré zaznamenávajú sled zlúčení a rozdelení, v ktorých vertikálna čiara predstavuje vzdialenosť medzi zhlukami, vzdialenosť medzi zvislými čiarami a vzdialenosť medzi zhlukami je priamo úmerná, tj čím väčšia je pravdepodobnosť, že zhluky budú rozdielne.
Pomocou dendogramu môžeme rozhodnúť o počte zhlukov, stačí nakresliť čiaru, ktorá sa na dendograme pretína s najdlhšou zvislou čiarou. Počet zvislých čiar, ktoré sa prekrývajú, bude počet zhlukov, ktoré sa majú zvážiť.
Nižšie je uvedený príklad dendogramu.
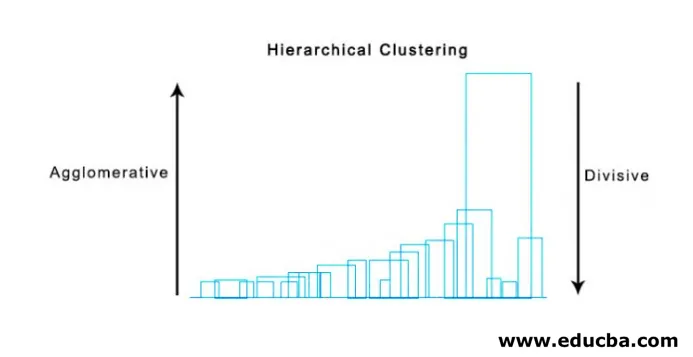
Existuje veľmi jednoduchý a priamy balík python a jeho funkcie slúžia na vykonávanie hierarchického zoskupovania a vykresľovania dendogramov.
- Hierarchia zo scipy.
- Cluster.hierarchy.dendogram pre vizualizáciu.
Bežné scenáre, v ktorých sa používa hierarchické zoskupovanie
- Segmentácia zákazníkov na marketing produktov alebo služieb.
- Územné plánovanie na identifikáciu miest na výstavbu štruktúr / služieb / budov.
- Analýza sociálnych sietí, napríklad, identifikujte všetkých fanúšikov MS Dhoni, aby ste propagovali jeho biopiku.
Výhody hierarchického zoskupovania
Výhody sú uvedené nižšie:
- V prípade čiastočného zhlukovania, ako je napríklad k-prostriedok, by mal byť počet zhlukov známy pred zhlukovaním, čo nie je možné v praktických aplikáciách, zatiaľ čo pri hierarchickom zhlukovaní sa nevyžaduje žiadna predchádzajúca znalosť počtu zhlukov.
- Hierarchické zoskupovanie vytvára hierarchiu, tj štruktúru, ktorá je viac informatívna ako neštruktúrovaná množina plochých zoskupení vrátených čiastočným zoskupovaním.
- Hierarchické zoskupovanie sa dá ľahko implementovať.
- Prináša výsledky vo väčšine scenárov.
záver
Typ zoskupovania predstavuje veľký rozdiel pri prezentácii údajov. Hierarchické zoskupovanie, ktoré je informatívnejšie a ľahšie analyzovateľné, sa uprednostňuje pred čiastočným zoskupovaním. A často sa spája s teplotnými mapami. Nezabudnite na atribúty vybrané na výpočet podobnosti alebo rozdielnosti, ktoré majú prevažný vplyv na zoskupenia aj hierarchiu.
Odporúčané články
Toto je sprievodca hierarchickým zoskupovaním. Tu diskutujeme úvod, výhody hierarchického zoskupovania a bežné scenáre, v ktorých sa hierarchické zoskupovanie používa. Viac informácií nájdete aj v ďalších navrhovaných článkoch -
- Clustering Algorithm
- Klastrovanie v strojovom učení
- Hierarchické zoskupovanie v R.
- Metódy zhlukovania
- Ako odstrániť hierarchiu v Tableau?