
Vzorec zloženej ročnej miery rastu (obsah)
- vzorec
- Príklady
- kalkulačka
Čo je vzorec zloženej ročnej miery rastu?
Zloženie je účinok, keď investícia získa úrok nielen z hlavnej zložky, ale aj z úroku. Zvýšená ročná miera rastu je teda efektívnym ročným rastom, ktorý sa dosiahol investíciou pri zohľadnení zloženia do obrazu. To v zásade predpokladá, že úroky získané každý rok sa reinvestujú a získa rovnaký úrok ako suma istiny. Z tohto dôvodu je zložená ročná miera rastu vždy vyššia ako jednoduchá úroková miera. Mnoho investícií, ako sú podielové fondy, návratnosť akciového trhu, nie sú príliš lineárne a veľmi nestabilné.
Kombinovaná ročná miera rastu pomáha pri vyrovnávaní tohto výnosu a povie, koľko investor zarobil počas doby investície vzhľadom na skutočnosť, že všetky výnosy medzi týmto obdobím sa reinvestujú rovnakou mierou. Vďaka tomuto efektu vyrovnávania nám pomáha pri porovnávaní súborov údajov s rôznou úrovňou volatility. Používa sa často na účely finančnej analýzy.
Konečná výška investície = počiatočná suma (1 + CAGR) počet rokov
Vzorec pre zloženú ročnú mieru rastu -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Tento vzorec je použiteľný, ak sa investícia každoročne zvyšuje, to znamená, že peniaze investujeme každý rok. Ale niekedy sa stáva, že chceme vypočítať mieru, v ktorej sa zloženie deje štvrťročne, mesačne, denne. Preto používame nasledujúci vzorec:
Konečná výška investície = počiatočná suma (1 + CAGR / zložená frekvencia) (počet rokov * kombinovaná frekvencia)
Vzorec pre zloženú ročnú mieru rastu -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Frekvencia zloženia:
- Polročné zloženie: 2
- Štvrťročné zloženie: 4
- Mesačná frekvencia: 12 a tak ďalej
Príklady vzorca CAGR (so šablónou programu Excel)
Vezmime príklad, aby sme lepšie pochopili výpočet vzorca CAGR.
Túto šablónu zloženého ročného tempa rastu Excel si môžete stiahnuť tu - šablónu zloženého ročného tempa rastuVzorec CAGR - príklad č. 1
Povedzme, že ste investovali 1 000 dolárov do podielových fondov pred 3 rokmi. Nasleduje návrat, ktorý ste dostali za tieto 3 roky:
- 1. rok ste dostali 20% zvýšenie hodnoty. Na konci prvého roka je teda celková hodnota 1 200 dolárov
- 2. rok ste získali 10% zvýšenie hodnoty. Celková hodnota je 1320 dolárov na konci druhého roka
- Tretí rok ste získali 10% zvýšenie hodnoty. Na konci 3. roku je teda celková hodnota 1452 dolárov
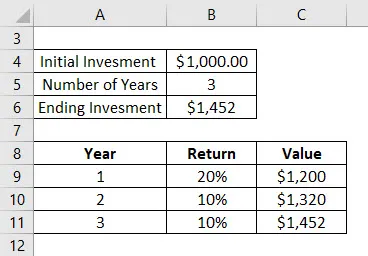
CAGR sa vypočíta pomocou vzorca uvedeného nižšie
CAGR = (konečná výška investície / počiatočná suma) (1 / počet rokov) - 1
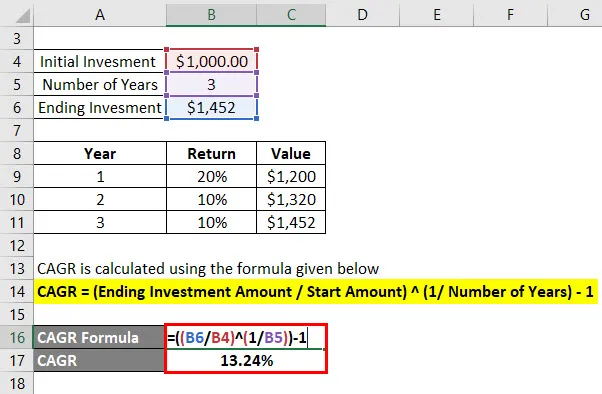
- CAGR = (1 452 $ / 1 000 USD) (1/3) -1
- CAGR = 13, 24%
Tu vidíme, že ročný výnos za všetky tri roky je odlišný a rôzny, ale zložená ročná miera rastu nám dáva jedinú mieru, ktorú môžeme porovnať s rôznymi investičnými príležitosťami.
Vzorec CAGR - príklad č. 2
Povedzme, že ste do banky investovali 1 000 dolárov a chcete peniaze v banke ponechať 4 roky. Teraz povedzme, že celková suma, ktorú získate po 4 rokoch, je 2 500 dolárov. Banka ponúka sadzbu s mesačným zložením. Vypočítajte CAGR.
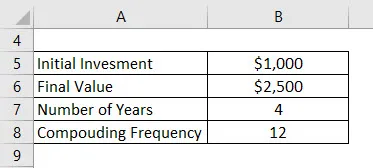
CAGR sa vypočíta pomocou vzorca uvedeného nižšie
CAGR = Frekvencia kombinovania * ((Konečná výška investície / Počiatočná suma) (1 / (Počet rokov * Frekvencia kombinovania)) - 1)
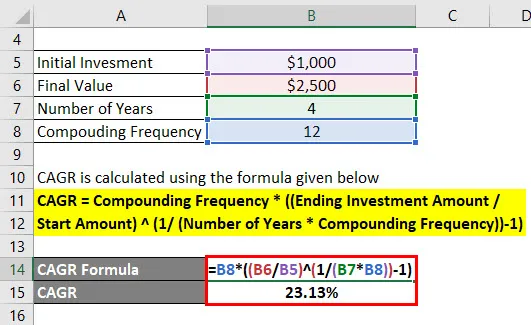
- CAGR = 12 * ((2 500 $ / 1 000 $) (1 / (4 * 12)) - 1)
- CAGR = 23, 13%
Kombinovaná ročná miera rastu je teda 23, 13%.
Vysvetlenie vzorca zloženej ročnej miery rastu
Aj keď zložená ročná miera rastu je ročnou mierou pre investíciu, predstavuje iba teoretickú hodnotu a nie je skutočnou návratnosťou. Hlavným predpokladom je, že všetky zisky sa reinvestujú s rovnakou mierou počas investičného obdobia, ale táto sadzba nezostane počas všetkých rokov a my nemusíme investovať svoje peniaze rovnakou mierou. Je to teda iba reprezentatívna sadzba, ktorá nám hovorí, že s čím by sme mohli skončiť, ak by sa všetky peniaze na konci každého roka opätovne investovali v tejto miere. Pri použití zloženej ročnej miery rastu by sme preto mali vziať do úvahy niektoré kľúčové body.
Budeme tiež skutočne opatrní pri investícii, ktorá je dlhá doba. Napríklad, ak je investičné obdobie veľmi dlhé, povedzme 20 rokov, zložená ročná úroková miera by nám mohla dať nesprávny náznak, pretože sa môže stať, že nezískame žiadny zisk počas prvých 15 rokov a všetky výnosy sa vrátia v poslednom období., Nezískanie zisku po dobu 15 rokov nie je prijateľné pre to, aby si ho udržali všetky podniky.
Podobne, ak majú dve investičné príležitosti rovnakú CAGR, môže sa stať, že jedna je viac priťahovaná ako druhá z dôvodu, že k rastu jednej dôjde v počiatočnom období, zatiaľ čo pre iné sa sústredí na konci tohto obdobia. obdobie.
Relevantnosť a použitie zloženého vzorca ročnej miery rastu
Zložená ročná miera rastu je skutočne užitočná pri výpočte priemernej miery rastu investície a môže pomôcť pri porovnávaní rôznych investícií. Ako sme videli v uvedenom príklade, medziročný rast investícií je nerovnomerný a nevyrovnaný. Ale pomocou zloženej ročnej miery rastu sa návratnosť vyhladí. Ďalším faktorom, ktorý robí zloženú ročnú mieru rastu kritickou metódou pri určovaní rastu investície, je skutočnosť, že zohľadňuje zložený účinok, ktorý ročná miera návratnosti nie je. Kombinovaná ročná miera nám neposkytuje skutočný obraz o výnosoch, pretože iba počíta návratnosť istiny a ignoruje úroky z úrokovej zložky, nie je to však prípad zloženej ročnej miery rastu.
Kalkulačka zloženej ročnej miery rastu
Môžete použiť nasledujúcu kombinovanú ročnú mieru rastu
| Konečná výška investície | |
| Počiatočná suma | |
| Počet rokov | |
| CAGR | |
| CAGR = | ((Konečná výška investície / počiatočná suma) 1 / počet rokov -1) |
| = | ((0/0) 1/0 -1) = 0 |
Odporúčané články
Toto bol sprievodca vzorcom zloženej ročnej miery rastu. Tu diskutujeme o výpočte CAGR spolu s praktickými príkladmi. Poskytujeme tiež zloženú ročnú mieru rastu s kalkulačkou Excel. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Sprievodca mierou návratnosti
- Príklady vzorca na exponenciálny rast
- Kalkulačka pre vzorec teórie centrálneho limitu
- Ako vypočítať kapitalizáciu trhu?