
Koeficient determinácie (obsah)
- vzorec
- Príklady
Čo je vzorec koeficientu determinácie?
V štatistike je koeficient určenia, tiež nazývaný ako R2, nástrojom, ktorý určuje a hodnotí schopnosť štatistického modelu vysvetliť a predpovedať budúce výsledky. Inými slovami, ak máme v modeli závislú premennú y a nezávislú premennú x, potom R2 pomáha pri určovaní variácie y pomocou variácie x. Je to jeden z kľúčových výstupov regresnej analýzy a používa sa, keď chceme predpovedať budúcnosť alebo testovať niektoré modely so súvisiacimi informáciami. Hodnota R2 je medzi 0 a 1 a vyššia hodnota R2, tým lepšia bude predpoveď a sila modelu. R2 je veľmi podobný korelačnému koeficientu, pretože korelačný koeficient meria priame priradenie dvoch premenných. R2 je v podstate štvorec korelačného koeficientu.
Vzorec pre koeficient určenia:
Na výpočet koeficientu stanovenia existuje niekoľko vzorcov:
- Použitie koeficientu korelácie:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Kde:
- X - Údajové body v množine údajov X
- Y - Dátové body v množine údajov Y
- - stredná hodnota dát
- Y m - Priemer sady údajov
tak
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Použitie výstupov regresie
Koeficient určenia (R2) = Vysvetlená variácia / celková variácia
Koeficient stanovenia (R2) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Kde:
- TSS - Celkový súčet štvorcov = Σ (Yi - Ym) 2
- MSS - modelový súčet štvorcov = Σ (Y - Ym) 2
- RSS - Zvyškový súčet štvorcov = Σ (Yi - Y ^) 2
Y je predpovedaná hodnota modelu, Yi je i-tá hodnota a Ym je stredná hodnota
Príklady koeficientu stanovenia (so šablónou Excel)
Vezmime príklad, aby sme lepšie pochopili výpočet koeficientu determinácie.
Túto šablónu koeficientu determinácie vzorca Excel si môžete stiahnuť tu - šablónu koeficientu determinácie vzorca ExcelKoeficient determinácie - príklad č. 1
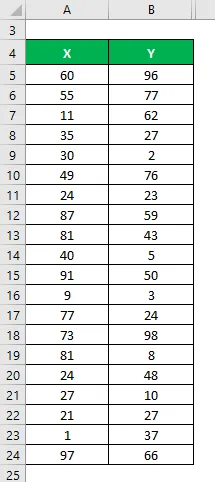
Povedzme, že máme dve sady údajov X a Y a každá obsahuje 20 náhodných údajových bodov. Vypočítajte koeficient stanovenia pre množinu údajov X a Y.
Priemer sa vypočíta ako:
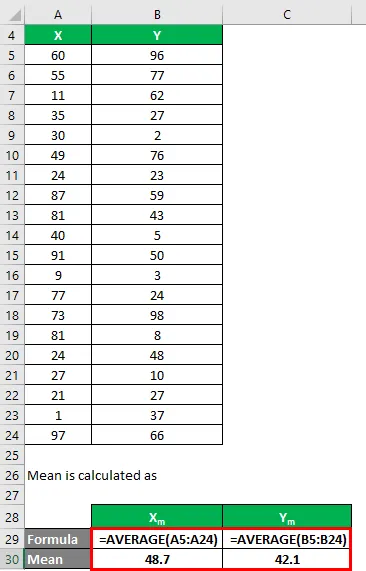
- Priemer dátového súboru X = 48, 7
- Priemer sady údajov Y = 42, 1
Teraz musíme vypočítať rozdiel medzi údajovými bodmi a strednou hodnotou.
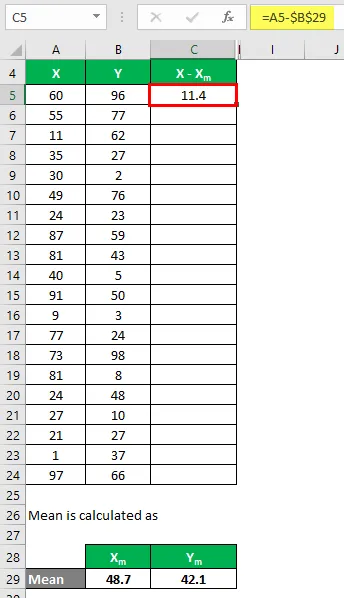
Podobne vypočítajte pre všetky súbory údajov X.
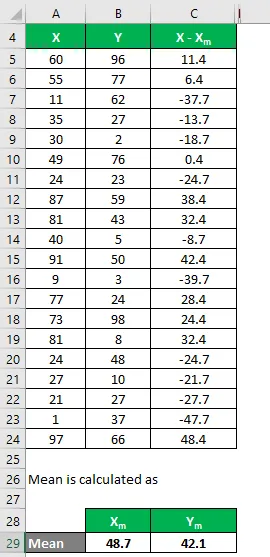
Podobne ho vypočítajte aj pre súbor údajov Y.

Vypočítajte druhú mocninu rozdielu pre súbory údajov X a Y.
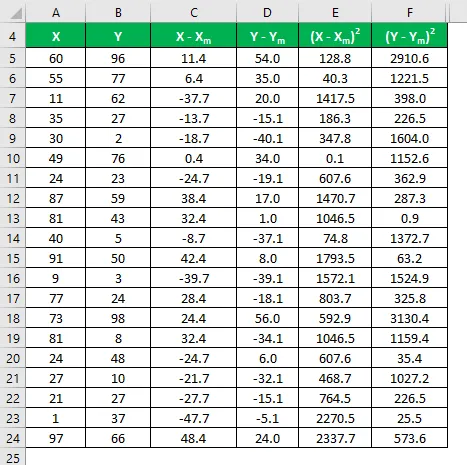
Vynásobte rozdiel v X s Y.
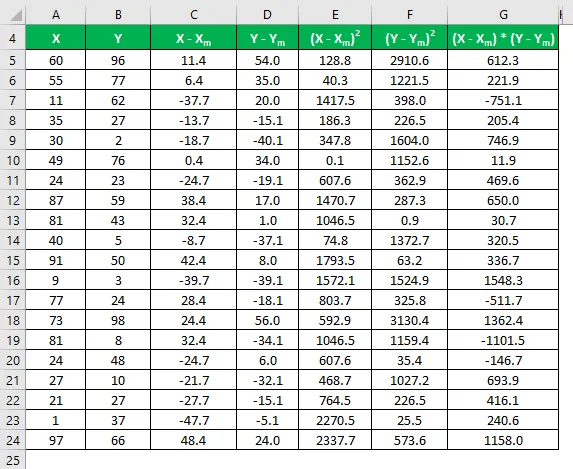
Korelačný koeficient sa vypočíta pomocou vzorca uvedeného nižšie
Korelačný koeficient = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
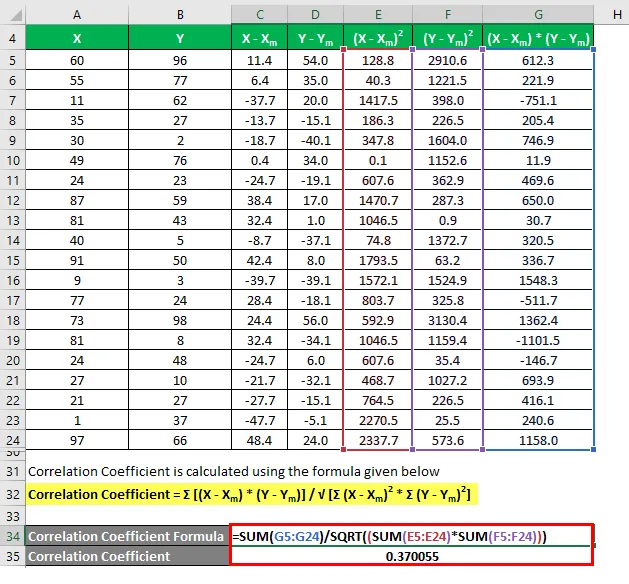
Koeficient stanovenia sa vypočíta pomocou vzorca uvedeného nižšie
Koeficient určenia = (Koeficient korelácie) 2
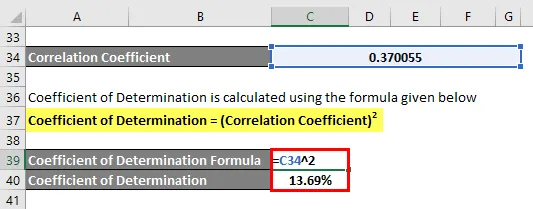
Koeficient určenia = 13, 69%
Koeficient determinácie - príklad č. 2
Povedzme, že ste veľmi averzným investorom proti riziku a hľadáte investovať peniaze na akciovom trhu. Nie ste si istí, do ktorých akcií investovať, a tiež vaša nízka riziková chuť do jedla. Takže chcete investovať do akcií, ktoré sú bezpečné a môžu napodobňovať výkonnosť indexu. Váš priateľ, ktorý je aktívnym investorom, pre vás vybral 3 akcie na základe ich základných a technických informácií a z týchto troch si chcete vybrať 2 akcie.
Zhromaždili ste tiež informácie o ich historických návratoch za posledných 15 rokov.
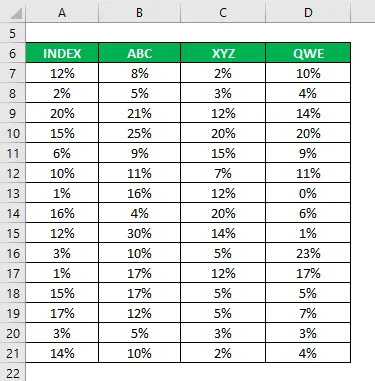
Korelačný koeficient sa počíta pomocou vynikajúceho vzorca
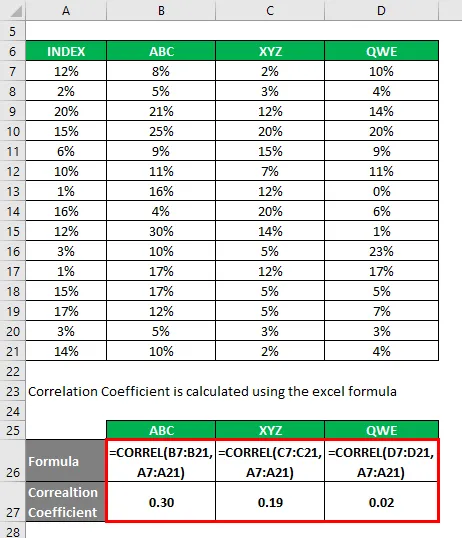
Koeficient stanovenia sa vypočíta pomocou vzorca uvedeného nižšie
Koeficient určenia = (Koeficient korelácie) 2
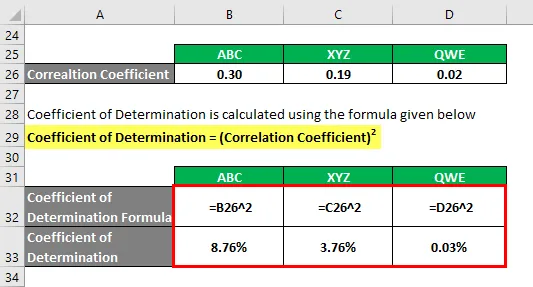
Na základe informácií si vyberiete akcie ABC a XYZ na investovanie, pretože majú najvyšší koeficient určenia.
vysvetlenie
Koeficient určenia, ako je vysvetlené vyššie, je druhou mocninou korelácie medzi dvoma súbormi údajov. Ak R2 je 0, znamená to, že neexistuje korelácia a nezávislá premenná nemôže predpovedať hodnotu závislej premennej. Podobne, ak je jeho hodnota 1, znamená to, že nezávislá premenná bude vždy úspešná pri predpovedaní závislej premennej. Existujú však aj určité obmedzenia. Aj keď nám hovorí o korelácii medzi 2 súbormi údajov, nehovorí nám, či je táto hodnota dostatočná alebo nie.
Tiež veľká hodnota R2 neznamená vždy, že tieto dve premenné majú silné vzťahy a môže to byť náhoda. Napríklad: Povedzme, že hodnota R2 medzi počtom predaných automobilov za rok a počtom krabíc so zmrzlinou predaných za rok je 80%. Medzi nimi však neexistuje žiadny vzťah. Pri použití R2 by sa preto malo postupovať veľmi opatrne, najskôr je potrebné porozumieť údajom a potom metódu použiť
Relevantnosť a použitie koeficientu určovania
Existuje veľa praktických aplikácií R2. Napríklad R2 investori veľmi často používajú na porovnávanie výkonnosti svojho portfólia s trhom a na predvídanie budúcich smerov. Podobne hedžové fondy používajú R2 a pomáhajú im modelovať riziko v ich modeloch. V konečnom dôsledku je však výsledok založený na čistých číslach a štatistikách, ktoré môžu byť niekedy zavádzajúce. Ako je uvedené vyššie, je potrebné najprv skontrolovať, či má výstup R2 zmysel v reálnom živote alebo nie.
Odporúčané články
Toto bol návod na výpočet koeficientu určovania. Tu diskutujeme o tom, ako vypočítať koeficient determinácie spolu s praktickými príkladmi a šablónou Excel na stiahnutie. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Sprievodca prípravou na trhové riziko
- Príklady vzorca pomeru pokrytia
- Kalkulačka pre výpočet nákladov na základe aktivity
- Ako vypočítať pomer informácií pomocou vzorca?