
Koeficient variácie vzorca (obsah)
- vzorec
- Príklady
Čo je to variačný koeficient?
V štatistike sa variačný koeficient nazýva aj CV ako nástroj, ktorý nám pomáha určiť, ako sa distribuujú údajové body v množine údajov okolo strednej hodnoty. V zásade sa najskôr vynesú všetky údajové body a potom sa variačný koeficient použije na meranie rozptylu týchto bodov od seba a priemeru. Pomáha nám to porozumieť údajom a tiež vidieť štruktúru, ktorú tvorí. Vypočíta sa ako pomer smerodajnej odchýlky súboru údajov k priemernej hodnote. Vyšší variačný koeficient znamená, že existuje väčšia miera rozptylu údajov okolo strednej hodnoty. Podobne, čím nižšia je hodnota variačného koeficientu, tým menšia je disperzia a presnejšie výsledky. Aj keď sa priemer dvoch dátových radov značne líši, variačný koeficient je veľmi užitočný na porovnanie stupňa variácie medzi jednotlivými dátovými radmi.
Vzorec pre variačný koeficient je daný:
Coefficient of Variation = Standard Deviation / Mean
Kroky na výpočet variačného koeficientu:
Krok 1: Vypočítajte priemer zo súboru údajov. Priemer je priemer všetkých hodnôt a možno ho vypočítať tak, že sa spočíta súčet všetkých hodnôt a potom sa vydelí počtom údajových bodov.
Krok 2: Potom vypočítajte smerodajnú odchýlku množiny údajov. To je trochu časovo náročný proces. Štandardná odchýlka sa môže vypočítať ako: √ (Σ (X i - X m ) 2 / (n - 1)) . X i je i-tý dátový bod a X m je stredná hodnota zo súboru údajov. Alternatívne nájdeme aj štandardnú odchýlku v Exceli pomocou funkcie STDEV.S ().
Krok 3: Rozdeľte smerodajnú odchýlku strednou hodnotou, aby ste dostali variačný koeficient.
Príklady koeficientu variácie (so šablónou programu Excel)
Urobme príklad, aby sme lepšie pochopili výpočet variačného koeficientu.
Túto šablónu koeficientu variácie vzorca Excel si môžete stiahnuť tu - šablónu koeficientu variácie vzorca ExcelKoeficient variácie - príklad č. 1
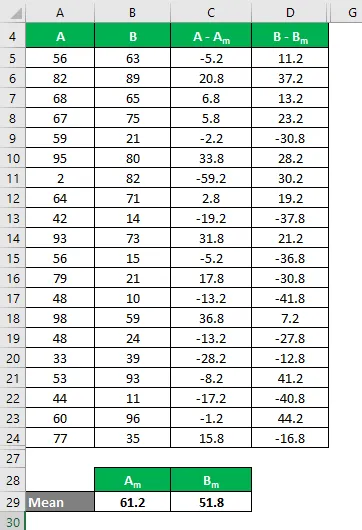
Povedzme, že máme dve sady údajov A a B a každá obsahuje 20 náhodných údajových bodov. Vypočítajte variačný koeficient pre množinu údajov X a Y.
Riešenie:
Priemer sa vypočíta ako:
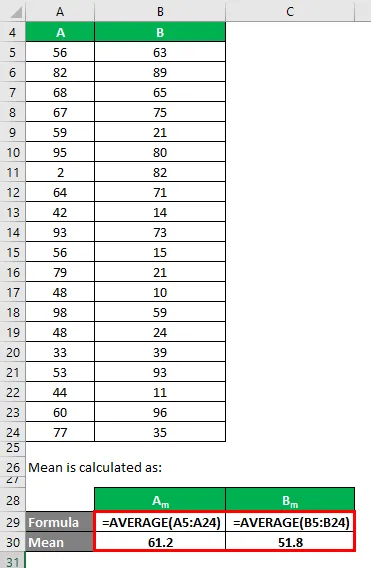
- Priemer dátového súboru A = 61, 2
- Priemer dátového súboru B = 51, 8
Teraz musíme vypočítať rozdiel medzi údajovými bodmi a strednou hodnotou.
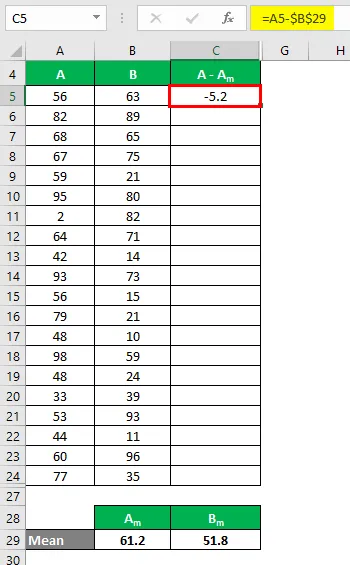
Podobne vypočítajte pre všetky hodnoty súboru údajov A.
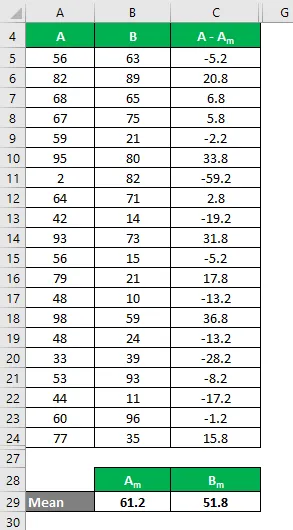
Podobne vypočítajte pre všetky hodnoty súboru údajov B.
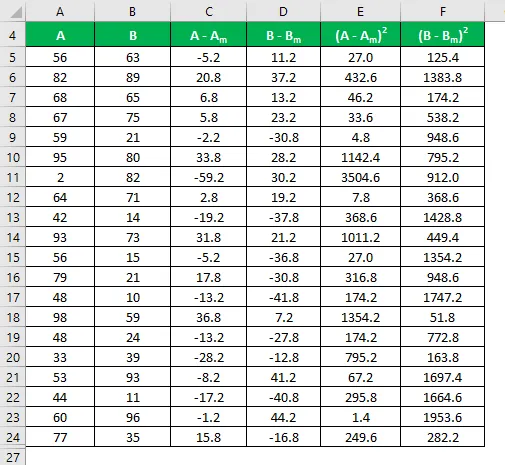
Vypočítajte druhú mocninu rozdielu pre súbory údajov A aj B.
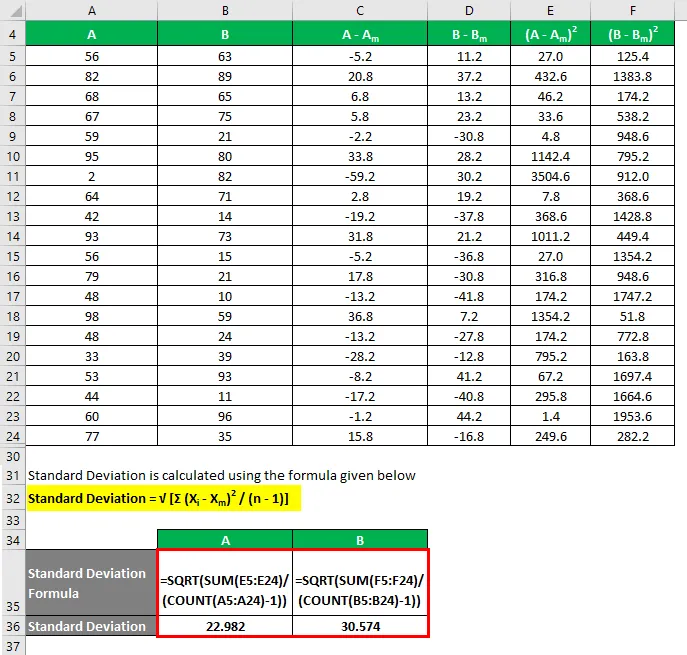
Štandardná odchýlka sa vypočíta pomocou vzorca uvedeného nižšie
Štandardná odchýlka = √ (Σ (X i - X m ) 2 / (n - 1))
Variačný koeficient sa vypočíta pomocou vzorca uvedeného nižšie
Variačný koeficient = smerodajná odchýlka / priemer
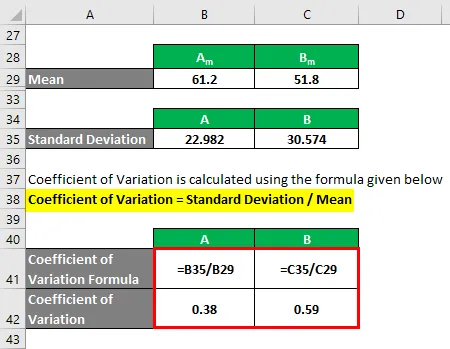
- Variačný koeficient A = 22, 982 / 61, 2 = 0, 38
- Variačný koeficient B = 30, 574 / 51, 8 = 0, 59
Ak tu vidíte, B má vyšší variačný koeficient ako A, čo znamená, že dátové body B sú viac rozptýlené ako A.
Koeficient variácie vzorca - Príklad č. 2
Povedzme, že ste veľmi averzným investorom proti riziku a hľadáte investovať peniaze na akciovom trhu. Keďže vaša nízka riziková chuť do jedla je nízka, chcete investovať do bezpečných akcií, ktoré majú nižšiu štandardnú odchýlku a variačný koeficient. Užšie ste vybrali 3 akcie na základe ich základných a technických informácií a chcete si vybrať 2 akcie. Zhromaždili ste tiež informácie o ich historických návratoch za posledných 15 rokov.
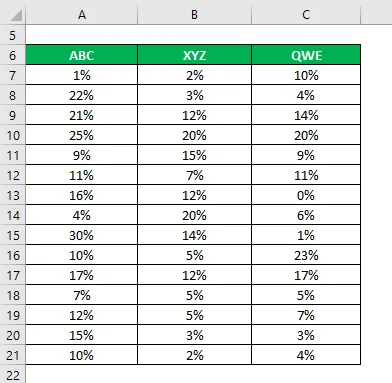
Riešenie:
Priemer sa vypočíta ako:
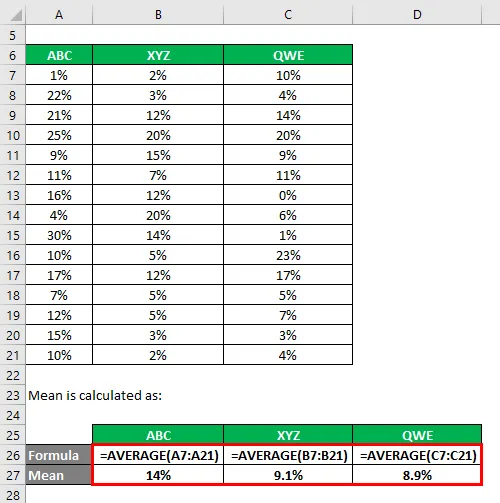
Štandardná odchýlka sa vypočíta pomocou vynikajúceho vzorca
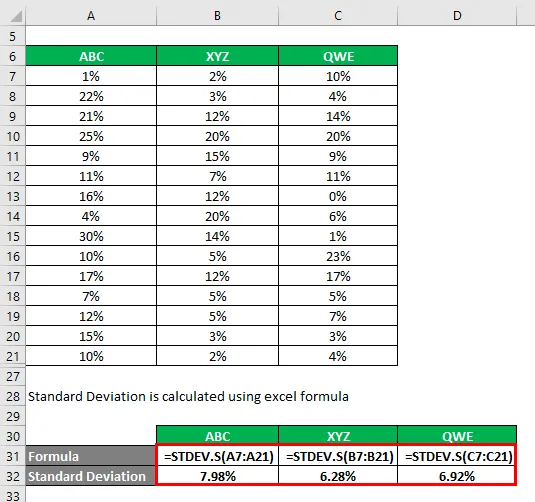
Variačný koeficient sa vypočíta pomocou vzorca uvedeného nižšie
Variačný koeficient = smerodajná odchýlka / priemer
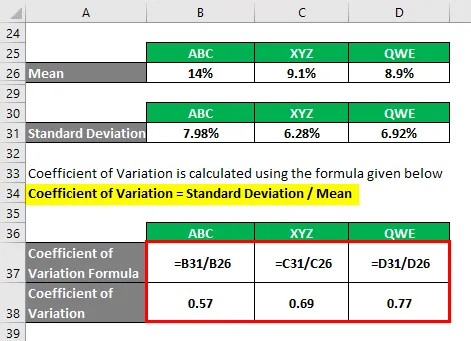
- Variačný koeficient ABC = 7, 98% / 14% = 0, 57
- Variačný koeficient XYZ = 6, 28% / 9, 1% = 0, 69
- Variačný koeficient QWE = 6, 92% / 8, 9% = 0, 77
Na základe týchto informácií si vyberiete akcie ABC a XYZ na investovanie, pretože majú najmenší variačný koeficient.
vysvetlenie
Keďže variačný koeficient je mierou rizika, pomáha pri meraní volatility cien akcií a iných finančných nástrojov. Pomáha tiež investorom a analytikom porovnávať riziká spojené s rôznymi potenciálnymi investíciami.
Variačný koeficient je podobný štandardnej odchýlke, ale štandardnú odchýlku dvoch premenných nemožno užitočne porovnávať. Ale použitie štandardnej odchýlky a priemeru robí relatívne porovnanie zmysluplnejším. Existuje tiež obmedzenie variačného koeficientu. Predpokladajme, že priemer množiny údajov je nula. V takom prípade sa tento nástroj stane neúčinným. Nielen to, ak máme súbor údajov, ktorý má veľa pozitívnych a negatívnych hodnôt, variačný koeficient sa stáva veľmi problematickým. Preto je užitočnejšie iba v prípade súborov údajov, ktoré majú rovnaké znamienko plus-mínus.
Relevantnosť a použitie koeficientu variácie
Koeficient variácie má význam v mnohých iných oblastiach ako štatistika. Napríklad v oblasti financií je variačný koeficient mierou rizika. Je to podobné štandardnej odchýlke, pretože sa používa aj ako miera rizika, ale rozdiel je v tom, že variačný koeficient je lepším ukazovateľom relatívneho rizika. Napríklad povedzme, že očakávaný výnos A je 15% a očakávaný výnos B je 10% a A má štandardnú odchýlku 10%, zatiaľ čo B má štandardnú odchýlku 5%. Na výber lepšej investície sa môže použiť variačný koeficient. Variačný koeficient A je 10/15 = 0, 666 a variačný koeficient B je 5/10 = 0, 5. Takže B je lepšia investícia ako A.
Odporúčané články
Toto bol sprievodca vzorcom koeficientu variácie. Tu diskutujeme o tom, ako vypočítať variačný koeficient pomocou vzorca spolu s praktickými príkladmi a stiahnuteľnou šablónou Excel. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Čo je upravený vzorec R na druhú?
- Príklady koeficientu stanovenia
- Ako vypočítať koeficient korelácie pomocou vzorca?
- Covariance Formula s Excel šablónou