
Rozdiel medzi skóre Z a skóre T
Z skóre je prevod prvotných údajov na štandardné skóre, keď je konverzia založená na priemernej populácii a štandardnej odchýlke populácie. Ak je u nás k dispozícii celý súbor údajov, môžeme vypočítať skóre Z. Z skóre je odpočítaním priemeru populácie od hrubého skóre a potom sa výsledok delí štandardnou odchýlkou populácie. T skóre je prevod prvotných údajov na štandardné skóre, keď je prevod založený na priemere vzorky a štandardnej odchýlke vzorky. Ak súbor údajov o populácii nie je k dispozícii, musíme si vybrať niektoré údaje zo vzorky, aby sme mohli vypočítať strednú hodnotu vzorky a štandardnú odchýlku populácie.
Skóre Z
Ak sú k dispozícii úplné údaje, pri normálnom rozdelení je to vzdialenosť od strednej hodnoty. Jeho vzorec je uvedený nižšie,
Z= (x-μ)/σ
Kde,
X = individuálne nespracované údaje
μ = priemerný počet obyvateľov
σ = smerodajná odchýlka populácie
Skóre T
T skóre je odpočítaním individuálnej štandardnej odchýlky od individuálneho priemeru a potom výsledok sa vydelí štandardnou odchýlkou vzorky celým výsledkom vynásobeným veľkosťou vzorky. Jeho vzorec je uvedený nižšie,
t = ((- μ)/s)*
= Priemer vzorky
μ = priemerný počet obyvateľov
s = vzorová smerodajná odchýlka
n = veľkosť vzorky
Vezmime príklad, aby sme to lepšie pochopili:
V príspevku sú uvedené tri pododdiely I, II a III. Nech je počet študentov, ktorí odpovedali, správne 25%, tj 75% to nedokáže správne odpovedať. Podobne nechajte 10% a 20% podľa počtu ľudí, ktorí odpovedali na oddiely II a III správne, takže 90% a 80% však našlo oddiely II a III. Predpokladáme, že schopnosť meraná týmito tromi položkami je rovnaká a je normálne distribuovaná,
Skóre pre každého študenta v triede sa používa na výpočet priemeru bodov, ktorý sa rovná 50 a štandardnej odchýlky 10. Môžeme vypočítať Z skóre so skóre 50 ako (50 - 50) / 10 = 0.
Môžeme interpretovať, že skóre študenta je 0 vzdialenosť (v jednotkách štandardných odchýlok) od priemeru, takže študent dosiahol priemer.
Ak je skóre 60, skóre Z je (60 - 50) / 10 = 1
Môžeme interpretovať, že študent dosiahol skóre nad priemerom - vzdialenosť 1 štandardnej odchýlky nad priemerom.
Porovnanie medzi dvoma bodmi medzi skóre Z a skóre T (infografika)
Nižšie je horných 9 rozdielov medzi skóre Z a skóre T 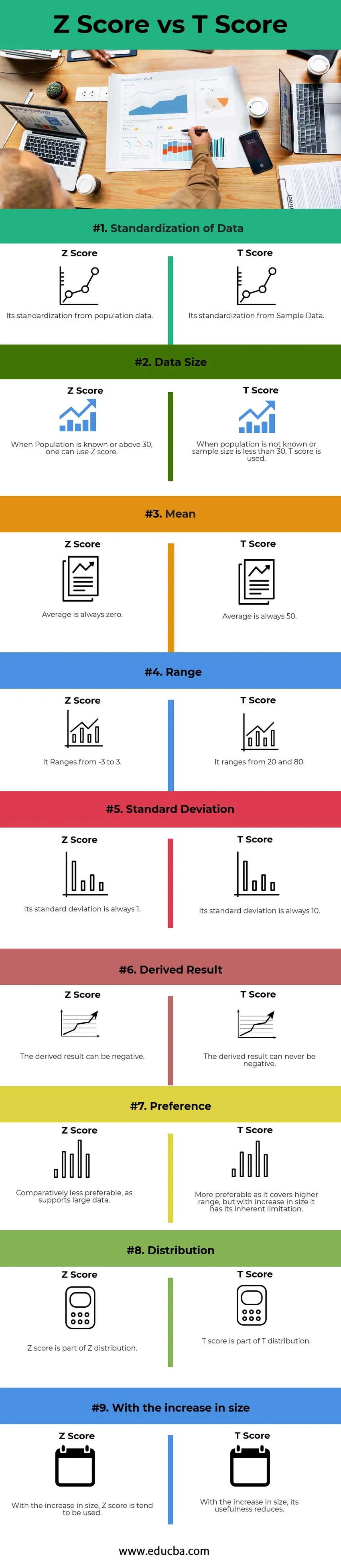
Kľúčové rozdiely medzi skóre Z a skóre T
Poďme diskutovať o niektorých hlavných rozdieloch medzi skóre Z a skóre T
- Z skóre je štandardizácia zo surových dát populácie alebo z viac ako 30 údajov vzorky na štandardné skóre, zatiaľ čo T skóre je štandardizácia z údajov vzorky menej ako 30 údajov na štandardné skóre
- Skóre Z sa pohybuje od -3 do 3, zatiaľ čo skóre T sa pohybuje od 20 do 80.
- Keď sa veľkosť dát zvyšuje, distribúcia má tendenciu byť distribúciou Z. Rozdelenie skóre Z skóre verzus T skóre je súčasťou normálneho rozdelenia, ale na základe veľkosti sa navzájom líšia
- Prakticky sa Z skóre vo veľkej miere používa v údajoch o akciovom trhu a na kontrolu šancí spoločnosti, ktorá sa dostane do bankrotu, zatiaľ čo t skóre sa vo veľkej miere používa pri kontrole hustoty minerálov kostí a hodnotení rizika zlomenín.
Porovnávacia tabuľka Z skóre vs. T skóre
Pozrime sa na prvých 9 Porovnanie medzi skóre Z a skóre T
| Č. | Porovnávacie body | Skóre Z | Skóre T |
| 1 | Štandardizácia údajov | Jeho štandardizácia z údajov o obyvateľstve | Jeho štandardizácia zo vzorových údajov |
| 2 | Veľkosť údajov | Ak je populácia známa alebo je vyššia ako 30, je možné použiť skóre Z | Ak nie je populácia známa alebo ak je veľkosť vzorky menšia ako 30, použije sa skóre T. |
| 3 | Priemerný | Priemer je vždy nula. | Priemer je vždy 50. |
| 4 | rozsah | To sa pohybuje od -3 do 3. | Je v rozsahu od 20 do 80. |
| 5 | Štandardná odchýlka | Jeho štandardná odchýlka je vždy 1 | Jeho štandardná odchýlka je vždy 10 |
| 6 | Odvodený výsledok | Odvodený výsledok môže byť negatívny | Odvodený výsledok nemôže byť nikdy negatívny |
| 7 | prednosť | Pomerne menej preferované, pretože podporuje veľké dáta | Výhodnejšie, pretože sa týka vyššieho rozsahu, ale so zväčšením má svoje vlastné obmedzenie |
| 8 | distribúcia | Skóre Z je súčasťou distribúcie Z | Skóre T je súčasťou distribúcie T |
| 9 | S nárastom veľkosti | Pri zväčšovaní veľkosti sa zvyčajne používa skóre Z | S nárastom jeho užitočnosti sa znižuje. |
záver
Obe Z skóre verzus T skóre sú súčasťou testovania hypotéz pri normálnom rozdelení. Ak máte skupinu meraní rôznych meraní pomocou Z-skóre, môžete povedať, ako sa skóre umiestňuje do ich distribúcií. Potom ich môžete porovnať. Normalizácia skóre je široko používaný postup v oblasti výskumu a plánovania, pretože pomáha pri porovnávaní rôznych skóre testu. Štandardizácia skóre pred ich kombináciou pomáha výskumnému pracovníkovi získať lepšie a porovnateľné výsledky.
Odporúčané články
Toto bol sprievodca najvyšším rozdielom medzi skóre Z a skóre T. Ďalej diskutujeme kľúčové rozdiely medzi skóre Z a skóre T s informačnou a porovnávacou tabuľkou. Môžete sa tiež pozrieť na nasledujúce články, kde sa dozviete viac -
- Financie vs ekonomika - najväčší rozdiel
- Deficit vs dlh - ktorý z nich je lepší
- Nákup aktív verzus nákup akcií
- Peňažný trh vs kapitálový trh
- Prehľad skóre Altmana Z