
Vzorec skóre Z (obsah)
- vzorec
- Príklady
- kalkulačka
Čo je to Z skóre?
„Z skóre“ je jedným z najpoužívanejších štatistických nástrojov, ktoré sa používajú na štandardizáciu skóre, za predpokladu, že sú známe populačné prostriedky a štandardná odchýlka. Z skóre je tiež známe ako štandardné skóre. Z skóre sa pohybuje v rozmedzí -3-násobku smerodajnej odchýlky až +3-násobku smerodajnej odchýlky so strednou hodnotou nula a štandardnou odchýlkou jedna. Vzorec pre skóre Z premennej možno odvodiť odpočítaním priemeru populácie od danej premennej (ktorá je súčasťou súboru údajov alebo populácie) a potom vydelením výsledku štandardnou odchýlkou populácie. Matematicky je reprezentovaný ako,
Z = (X – μ) / σ
kde,
- X = premenná z počtu obyvateľov
- μ = Priemerný počet obyvateľov
- σ = smerodajná odchýlka populácie
Príklady vzorca na výpočet skóre Z (so šablónou programu Excel)
Vezmime príklad, aby sme lepšie pochopili výpočet skóre Z.
Túto šablónu Z Score Formula Excel si môžete stiahnuť tu - Z Score Excel Excel TemplateVzorec skóre Z - príklad č. 1
Vezmime príklad Mannyho, ktorý sa nedávno objavil pre SAT. V tomto pokuse sa mu podarilo dosiahnuť 1109 bodov. Podľa dostupných informácií však priemerné skóre pre SAT zostalo okolo 1030 so štandardnou odchýlkou 250. Vypočítajte skóre Z pre skóre SAT od Mannyho a zhodnoťte, ako dobre sa daril v porovnaní s priemernými účastníkmi testu.
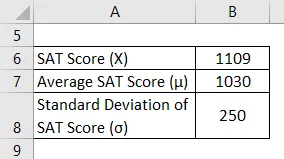
Riešenie:
Z Skóre sa vypočíta pomocou vzorca uvedeného nižšie
Z = (X - μ) / σ
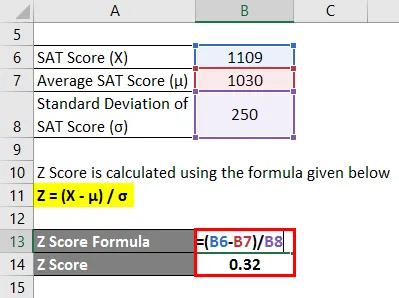
- Z skóre = (1109 - 1030) / 250
- Skóre Z = 0, 32
Preto je skóre SAT Mannyho o 0, 32 štandardnej odchýlky vyššie ako priemerné skóre testujúcich účastníkov, čo naznačuje, že 62, 55% účastníkov testu malo menej ako Manny.
Vzorec skóre Z - príklad č. 2
Teraz si ukážme príklad Chelsea, ktorá napísala SAT dvakrát a chce v nich porovnať jej výkon. Vo svojom 1. a 2. pokuse dokázala skórovať 1085 a 1059. Podľa dostupných informácií bolo priemerné skóre a štandardná odchýlka počas prvého pokusu 1100 a 230, zatiaľ čo v druhom prípade to bolo 1050 a 240. Pomôžte Chelsea rozhodnúť sa, v ktorej skúške dosiahla lepšiu výkonnosť.
Riešenie:
1. pokus
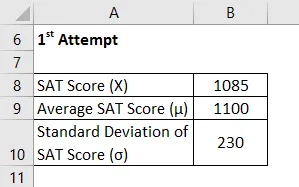
Z Skóre sa vypočíta pomocou vzorca uvedeného nižšie
Z = (X - μ) / σ
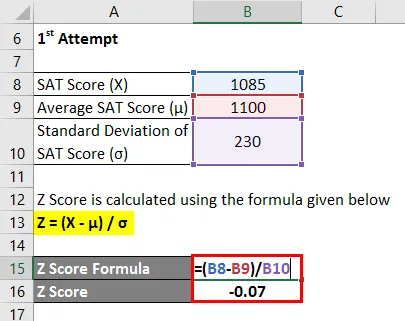
- Z skóre = (1085 - 1100) / 230
- Z skóre = -0, 07
Preto je skóre SAT Chelsea v prvom pokuse o 0, 07 smerodajná odchýlka nižšia ako priemerné skóre testovacieho príjemcu, čo naznačuje, že 47, 40% testovaných účastníkov získalo menej ako Chelsea počas prvého pokusu.
2. pokus
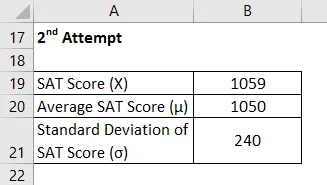
Z Skóre sa vypočíta pomocou vzorca uvedeného nižšie
Z = (X - μ) / σ
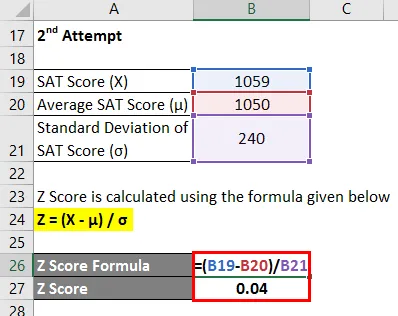
- Z skóre = (1059 - 1050) / 240
- Skóre Z = 0, 04
Preto je skóre SAT Chelsea v 2. pokuse o 0, 04 štandardná odchýlka vyššia ako priemerné skóre testujúcich príjemcov, čo naznačuje, že 51, 50% testovaných účastníkov získalo menej ako Chelsea počas druhého pokusu.
Z porovnania skóre Z je teda zrejmé, že Chelsea sa počas druhého pokusu správala lepšie.
vysvetlenie
Vzorec pre skóre Z možno odvodiť pomocou nasledujúcich krokov:
Krok 1: Najskôr sa zostaví populácia s veľkým počtom premenných a premenné sa označia Xi.
Krok 2: Ďalej sa vypočíta počet premenných v populácii a označí sa N.
Krok 3: Ďalej sa priemer populácie vypočíta spočítaním všetkých premenných a potom delením celkovým počtom premenných (krok 2) v súbore údajov. Priemer populácie sa označuje μ.
μ = ∑ X i / N
Krok 4: Ďalej odpočítajte priemer z každej premennej súboru údajov, aby ste vypočítali ich odchýlku od priemeru.
tj (X i - μ) je odchýlka pre i- tý dátový bod.
Krok 5: Ďalej vypočítajte štvorcové odchýlky pre premenné, tj (Xi - μ) 2 .
Krok 6: Ďalej spočítajte všetky štvorcové odchýlky a potom vydeľte súčet počtom premenných v množine údajov, aby ste dospeli k rozptylu.
σ 2 = ∑ (Xi - μ) 2 / N
Krok 7: Ďalej sa štandardná odchýlka populácie vypočíta výpočtom druhej odmocniny rozptylu vypočítaného v predchádzajúcom kroku.
σ = √ ∑ (Xi - μ) 2 / N
Krok 8: Nakoniec sa vzorec pre skóre Z odvodí odpočítaním priemeru populácie (krok 3) z premennej a následným vydelením výsledku štandardnou odchýlkou populácie (krok 7), ako je uvedené nižšie.
Z = (X - μ) / σ
Relevantnosť a použitie vzorca Z Score
Z pohľadu štatistika je pojem Z skóre veľmi dôležitý, pretože je užitočný pri určovaní pravdepodobnosti, či sa udalosť vyskytne v rámci normálneho rozdelenia. V skutočnosti sa Z skóre tiež používa na porovnanie dvoch nespracovaných skóre z dvoch rôznych normálnych distribúcií a robí sa prevodom nespracovaných skóre na skóre Z alebo štandardizované skóre. Ďalej, pozitívne skóre Z znamená skóre, ktoré je vyššie ako priemer, zatiaľ čo záporné skóre Z znamená skóre nižšie ako priemer.
Kalkulačka skóre skóre Z
Môžete použiť nasledujúcu kalkulačku skóre skóre Z
| X | |
| μ | |
| σ | |
| Z | |
| Z = |
|
|
Odporúčané články
Toto bol sprievodca Z Score Formula. Tu diskutujeme o tom, ako vypočítať skóre Z spolu s praktickými príkladmi. Poskytujeme tiež kalkulačku skóre Z s šablónou Excel na stiahnutie. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Príklady vzorcov pre veľkosť vzoriek
- Ako vypočítať vážený priemer?
- Kalkulačka pre korelačný vzorec
- Vzorec na výpočet normálnej distribúcie
- Príklady skóre Altmana Z