Vzorec efektívnej ročnej sadzby (obsah)
- vzorec
- Príklady
- kalkulačka
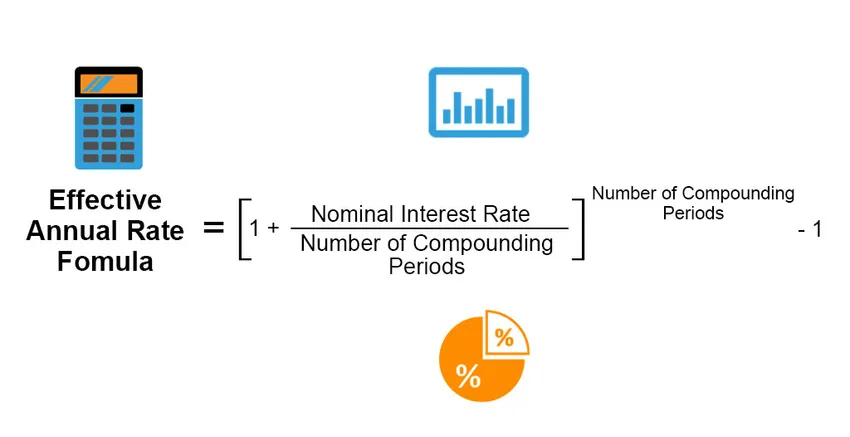
Aký je vzorec efektívnej ročnej sadzby?
Efektívna ročná sadzba je skutočná úroková sadzba, ktorá je získaná alebo vyplatená z investície, úveru alebo iného podobného finančného produktu, a inak sa líši od „nominálnej úrokovej sadzby“ z dôvodu výplaty úroku, zloženia úrokovej sadzby, celkom časové obdobie úveru alebo investície atď. Efektívna ročná sadzba sa vypočíta podľa nasledujúceho vzorca;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Príklady vzorca efektívnej ročnej sadzby (so šablónou programu Excel)
Vezmime príklad, aby sme lepšie pochopili výpočet efektívnej ročnej sadzby.
Túto šablónu efektívnej ročnej sadzby vzorca Excel si môžete stiahnuť tu - šablónu efektívnej ročnej sadzby vzorca ExcelVzorec efektívnej ročnej sadzby - príklad č. 1
Predpokladajme, že pán X si vezme osobnú pôžičku od banky s úrokovou sadzbou 20%, ktorá sa každoročne zloží. Vypočítajte efektívnu ročnú mieru pomocou týchto informácií.

Riešenie:
Efektívna ročná sadzba sa vypočíta pomocou vzorca uvedeného nižšie
Efektívna ročná sadzba = ((1 + (nominálna úroková sadzba / počet kombinovaných období)) počet kombinovaných období) - 1

- Efektívna ročná miera = ((1 + (20% / 2)) 2) - 1
- Efektívna ročná sadzba = 21%
Vzorec efektívnej ročnej sadzby - príklad č. 2
Predpokladajme, že pán A investoval 100 dolárov do vkladového certifikátu, ktorý vypláca nominálnu ročnú úrokovú sadzbu 10% znásobenú štvrťročne. Vypočítajte skutočnú ročnú mieru.

Riešenie:
Efektívna ročná sadzba sa vypočíta pomocou vzorca uvedeného nižšie
Efektívna ročná sadzba = ((1 + (nominálna úroková sadzba / počet kombinovaných období)) počet kombinovaných období) - 1
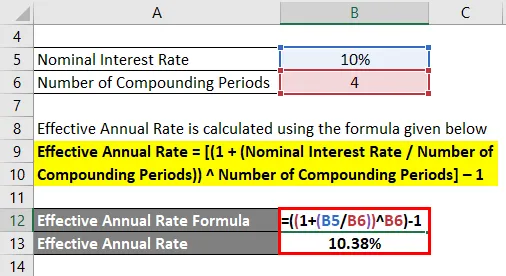
- Efektívna ročná miera = ((1 + (10% / 4)) 4) - 1
- Efektívna ročná miera = 10, 38%
Vzorec efektívnej ročnej sadzby - príklad č. 3
Predpokladajme, že investície do podielových fondov vyvolávajú ročnú úrokovú sadzbu 15, 50% ako zisk, zatiaľ čo pôžičky P2P získavajú ročnú nominálnu úrokovú sadzbu 15%, ktorá sa zvyšuje mesačne. Vypočítajte teda skutočnú ročnú sadzbu pre oba prípady.

Riešenie:
Efektívna ročná sadzba sa vypočíta pomocou vzorca uvedeného nižšie
Efektívna ročná sadzba = ((1 + (nominálna úroková sadzba / počet kombinovaných období)) počet kombinovaných období) - 1
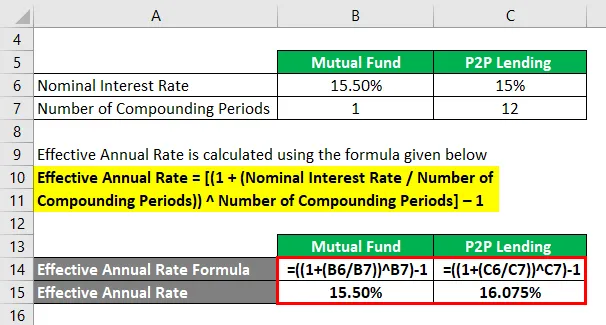
Pre podielový fond
- Efektívna ročná miera = ((1 + (15, 50% / 1)) 1) - 1
- Efektívna ročná miera = 15, 50%
Pre pôžičky P2P
- Efektívna ročná miera = ((1 + (15% / 12)) 12) - 1
- Efektívna ročná miera = 16, 075%
vysvetlenie
Nominálna úroková sadzba je uvedená sadzba finančného produktu. V príklade 3 nominálna sadzba zobrazená na produktoch spôsobuje, že podielový fond vyzerá ako preferovaná voľba pre investorov, pretože ročná nominálna úroková miera je o 0, 50% vyššia.
Efektívna ročná sadzba sa však počíta tak, že sa vezme nominálna ročná úroková miera a zloží sa za počet stanovených období (12, ak je zloženie mesačné; 6, ak je zloženie dvojmesačné; 4, ak je štvrťročné, a 2, ak je zložené je polročné) použiteľné v časovom rozpätí jedného roka. V prípade podielového fondu je počet období zloženia za rok 1, zatiaľ čo v prípade pôžičiek P2P je to mesačné zloženie, preto existuje 12 období zloženia.
Na základe vzorca
Efektívne ročné výnosy = ((1 + (nominálna úroková sadzba / počet kombinovaných období)) (počet kombinovaných období)) - 1
Efektívna ročná návratnosť podielového fondu = ((1 + (15, 50% / 1)) 1) - 1 = 15, 50%
Efektívny ročný výnos požičiavania P2P = ((1 + (15, 00% / 12)) 12) - 1 = 16, 075%
Relevantnosť a použitie vzorca efektívnej ročnej sadzby
Vzorec efektívnej ročnej sadzby sa používa na rozlíšenie skutočnej IRR (Interná miera návratnosti) alebo anualizovaného výnosu pre úrokovú sadzbu, ktorá sa môže alebo nemusí v danom období viackrát zložiť. To by sa mohlo veľmi dobre použiť pri porovnávaní rôznych druhov investičných príležitostí alebo pôžičiek poskytnutých v rôznych štruktúrach.
Predpokladajme, že existujú 2 investičné príležitosti, termínované vklady pošta a fixné vklady, na ktoré sa investor zúžil, vzhľadom na jeho rizikový apetít a vhodnosť. Konečným cieľom investora je čo najlepšie využiť tieto vklady a získať vyššiu návratnosť. Oba nástroje však ponúkajú mierne odlišné úrokové sadzby, zatiaľ čo termínovaný vklad pošta ponúka štvrťročné zloženie za uvažované obdobie.
- Výška investície: Rs. 10 lakh
- Investičné obdobie: 5 rokov
- Pevný vklad v banke: 7, 5% ročný úrok
- Termínovaný vklad pošta: 7, 4% ročný úrok, zložený štvrťročne
Z hľadiska ponúkaných ročných úrokových sadzieb sa zdá byť lepšou voľbou pevný vklad v banke. Ak však investor skutočne počíta štvrťročný faktor zloženia termínovaného vkladu pošta, výsledkom bude efektívna ročná miera / výnos 7, 61%.
V dôsledku tejto malej zmeny efektívnej sadzby zo 7, 4% na 7, 61% by investor zarobil celkom Rs. 4, 42, 848, 28 z tohto konkrétneho nástroja, zatiaľ čo on / ona by si zarobil Rs. 3, 35, 469, 14 z nástroja pevného vkladu banky.
Keby investor neuskutočnil výpočet tejto efektívnej ročnej sadzby, stratil by príležitosť získať približne viac ako Rs. 1 lakh z jeho investície.
Efektívna kalkulačka ročných sadzieb
Môžete použiť nasledujúcu efektívnu kalkulačku ročných sadzieb
| Nominálna úroková sadzba | |
| Počet období zloženia | |
| Efektívna ročná sadzba | |
| Skutočná ročná miera | ((1 + (nominálna úroková sadzba / počet kombinovaných období)) Počet kombinovaných období ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 |
Odporúčané články
Toto je sprievodca vzorcom efektívnej ročnej sadzby. Tu diskutujeme o tom, ako vypočítať efektívnu ročnú mieru spolu s praktickými príkladmi. Poskytujeme tiež efektívnu ročnú sadzbu kalkulačky s možnosťou stiahnutia z Excel šablóny. Ďalšie informácie nájdete aj v nasledujúcich článkoch -
- Kalkulačka vzorca reálnej úrokovej sadzby
- Receptúra návratnosti kapitálu definícia
- Ako vypočítať efektívnu úrokovú sadzbu?
- Čo je súčasná hodnota vzorca dôchodkov?