
Úvod do algoritmu kreslenia čiar
V tomto článku sa zobrazí obrys algoritmu na kreslenie čiar. Čiara v počítači znamená, že obrazovka počítača sa delí na dva riadky a stĺpce. Tieto riadky a stĺpce sú známe aj ako pixely. V prípade, že musíme na počítači nakresliť čiaru, musíme vedieť, na ktorých pixeloch by mali byť. Čiara je časť priamky, ktorá sa šíri v opačnom smere na neurčito. Čiara je definovaná dvoma koncovými bodmi. Jeho hustota by mala byť oddelená od dĺžky vlasca.
Vzorec na priamkové zachytenie svahu: Y = mx + b
V tomto vzorci m je priamka svahu a b je priesečník y v priamke. V pozíciách (x1, y1) a (x2, y2) sa pre segment úsečky určujú dva koncové body.
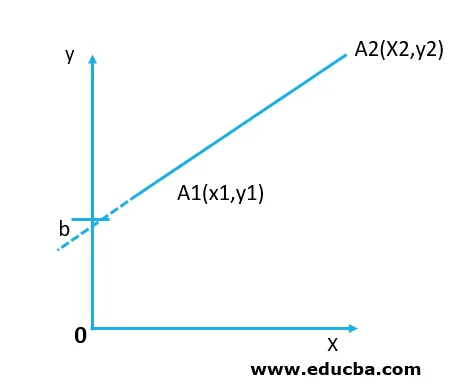
Hodnota sklonu ma ab môže byť stanovená zodpovedajúcim spôsobom
• m = y2 - y1 / x2 - x1
• tj M = Δy / Δx
Príklad:
Koncové body riadkov sú (0, 0) a (4, 12). Výsledok vyneste na výpočet každej hodnoty y ako kroky x od 0 do 4.
Riešenie:
Takže máme vzorec rovnice priamky: Y = mx + b
• m = y2 - y1 / x2 - x1
• m = 12 - 0 - 4 - 0
• m = 3
Priesečník y sa potom nájde spojením y1 a x1 so vzorcom y = 3 x + b, 0 = 3 (0) + b. Preto b = 0, takže y = 3x riadok.
Cieľom je určiť najbližšie miesto x, y čo najrýchlejšie tým predchádzajúcim.
Typy algoritmov na kreslenie čiar
Nižšie sú uvedené typy algoritmov:
1. Digitálny diferenciálny algoritmus (DDA)
Metóda inkrementálnej konverzie je algoritmus DDA a nazývame sa aj digitálny diferenciálny algoritmus (DDA). Tento prístup je charakterizovaný použitím výsledkov z predchádzajúcej fázy v každom výpočte.
Pozrime sa na príklady uvedené nižšie:
Príklad č. 1
Čiara koncového bodu je (x1, y1) a (x2, y2)
- dx = x2 - x1
- dy = y2 - y1
takže teraz určíme dĺžku čiary, ak abs (dx)> = abs (dy), potom dĺžka = abs (dx) inak length = abs (dy)
- Δx = dx / dĺžka
- Δy = dy / dĺžka
- X = x1
- Y = y1
Setpixel (kolo (x), kolo (y));
- i = 1
zatiaľ čo (i <= dĺžka)
- x = x + Ax;
- y = y + y;
setpixel (kolo (x), kolo (y));
i = i + 1
koniec
Príklad č. 2
DDA môže byť konvertovaná línia koncových bodov (5, 4) a (6, 9).
Riešenie:
• dx = x2 - x1
• dx = 6 - 5 = 1
• dy = y2 - y1
• dy = 9 - 4
dy = 5
Ako, dx <dy potom,
• length = y2 - y1 = 5
• dx = (x2 - x1) / dĺžka = 1/5 = 0, 2
• dy = (y2-y1) / length = 5/5 = 1
x1 y1 x2 y2 L dx dy ixy
result:
X1 |
Y1 |
X2 |
Y2 |
L |
dx |
D Y |
ja |
X |
Y |
výsledok |
3 |
2 |
4 |
7 |
5 |
0, 2 |
1 |
0 |
3.5 |
5.5 |
3, 5, 5, 5 |
1 |
3.9 |
1.5 |
3.9, 1.5 |
|||||||
2 |
4.9 |
3.5 |
4.9, 3.5 |
|||||||
3 |
5.1 |
7.5 |
5.1, 7.5 |
|||||||
4 |
3.7 |
4.5 |
3.7, 4.5 |
|||||||
5 |
4.5 |
7.5 |
4.5, 7.5 |
Obmedzenie algoritmu DDA
- Aritmetika pre plávajúce a zaokrúhľovacie body sú časovo náročné postupy.
- Chyba zaokrúhľovania môže viesť k vzdialenosti od skutočnej dráhy segmentu dlhej čiary podľa umiestnenia meraného pixla.
2. Algoritmus Bresenhamovej línie
Algoritmus konverzie skenovania je Bresenhamov algoritmus. Tento algoritmus ponúka hlavnú výhodu použitia iba celočíselných výpočtov.
1. Koncové body riadku a uložte ľavý koncový bod do (x1, y1)
2. Pre rozhodovací parameter sa získa prvá hodnota Δx tj Dx, Δy tj Dy, 2 Δy a 2 x.
3. Inicializujte spustenie
4. Inicializujte i = 1 ako počítadlo,
Inak je ďalší bod, ktorý sa má vykresliť, (xk + 1, yk + 1) a opakujte krok 4 (Ax - 1) krát.
nastavenie
Pre m> 1 môžeme povedať, že ak x zväčšíme y, x sa zvýši.
Po rozhodnutí rozhodovacej premennej pk bude vzorec veľmi podobný, nahradia sa iba xay v rovnici.
Zhrnutie algoritmu Bresenhamovej línie
Toto sú nasledujúce výhody algoritmu Bresenhamovej línie:
• Rýchly prírastkový algoritmus.
• Používa sa iba celé číslo.
DDA má pri porovnaní s algoritmom DDA nasledujúce problémy:
• Pixelovaná čiara môže byť vzdialená od očakávaného hromadenia chýb zaokrúhľovania.
• Čas potrebný na zaokrúhľovanie a aritmetický postup s pohyblivou rádovou čiarkou.
Odporúčané články
Toto bol sprievodca Algoritmom kreslenia čiar. Tu diskutujeme o tom, čo je algoritmus kreslenia čiar spolu s rôznymi príkladmi. Ak sa chcete dozvedieť viac, môžete si pozrieť aj nasledujúce články -
- Algoritmy strojového učenia
- Algoritmus SVM
- Jednoduchá lineárna regresia
- Viacrozmerná regresia
- Najlepšie porovnanie lineárnej regresie s logistickou regresiou