Komplexné čísla v MATLABe Ako vygenerovať komplexné číslo?

Úvod do komplexných čísel v MATLABe

Komplexné čísla sú kombináciou reálnych čísel a imaginárnych čísel vo forme p + qi, kde p a q sú skutočné čísla a i je imaginárne číslo. Predstavuje sa imaginárne číslo, kde i je výsledok rovnice a 2 = -1. Môžeme použiť i alebo j na označenie imaginárnych jednotiek. Pretože zložité čísla sa používajú v akýchkoľvek matematických výpočtoch a Matlab sa používa hlavne na vykonávanie matematických výpočtov. Takže komplexné čísla sú dôležitou súčasťou učenia sa Matlabu.

Generovanie komplexných čísel v MATLABe

Komplexné čísla môžu byť vytvorené alebo deklarované v Matlabe pomocou „komplexnej“ funkcie. Môžeme tiež vytvoriť komplexné čísla nájdením druhej odmocniny záporného čísla. V Matlabe môžeme pomocou i alebo j označiť pomyselnú časť komplexného čísla.

Príklady

X = 4 + 5i

X je komplexné číslo, ktoré obsahuje 2 časti, tj skutočnú a imaginárnu časť. 4 je skutočná časť a 5 je imaginárna časť. Skutočné a imaginárne časti nájdeme pomocou funkcií v Matlabe.

a = reálna (X) = 4 (udáva skutočnú časť komplexného čísla)
b = imag (X) = 5 (Poskytuje imaginárnu časť komplexného čísla)
komplex (6, 7) = 6 + 7i (Táto funkcia sa používa na vytvorenie komplexného čísla)

Môžeme tiež vytvoriť komplexné polia v Matlabe, ktoré sa dajú deklarovať aj pomocou komplexných funkcií.

a = komplex (x, y)

Existujú určité podmienky pre xay, ktoré by sme mali dodržiavať, pretože x a y by nemali byť jednoduché alebo dvojité. Komplexný skalár sa dá vytvoriť, ak majú dva vstupy skalárny charakter,

X = komplex (5, 3)
X = 5, 0000 + 3, 0000i

Podobne je možné vytvoriť komplexný vektor, ak máme dva vstupy ako vektory.

X = uint8 ((4, 5, 6, 7));
Y = uint8 ((3, 5, 1, 2));
a = komplex (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Môžeme vytvoriť komplexné číslo, ktoré má iba jednu skalár,

X = komplex (10)
X = 10, 0000 + 0, 0000i

Existujú určité podmienky, ktoré by mali vstupné a výstupné argumenty nasledovať,

Vstupné argumenty obsahujú reálne a imaginárne časti ako x ľubovoľný y. xay by mali byť skalárne, vektorové, viacrozmerné pole alebo matica v MATLABe. Veľkosť xay by mala byť rovnaká. Mali by byť rovnakého typu údajov, ale existuje niekoľko výnimiek, ako je dvojnásobok, ktorý sa dá použiť s jedným a celé číslo sa môže kombinovať s dvojitým, ktorý je skalárny.

Výstupom poľa môže byť vektorové, skalárne, maticové alebo viacrozmerné pole v závislosti od vstupných argumentov. Veľkosť výstupu by mala byť rovnaká ako vstup. Ak sú vstupné argumenty rôznych typov údajov, ako je výstup určený,

Ak je niektorý zo vstupných argumentov jednoduchý, výstup by mal byť aj jednoduchý.
Ak je niektorý zo vstupných argumentov prirodzene celé číslo, výstup by mal byť typu celočíselného typu.

Môžeme skontrolovať, či je matica reálna alebo imaginárna pomocou izrealickej funkcie.

kód:

X = (2+i, 1); Isreal(X)

Výkon:

kód:

Isreal (X (2))

Výkon:

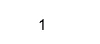
Na extrahovanie skutočných a imaginárnych častí môžeme v Matlabe použiť skutočné a imaginárne funkcie,

kód:

real(X)

Výkon:

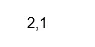
kód:

imag(X)

Výkon:

Operácie a funkcie komplexných čísel v MATLABe

Existuje niekoľko operácií a funkcií, ktoré je možné vykonávať pomocou zložitých čísel v Matlabe ako

abs: Táto funkcia sa používa na nájdenie modulu ľubovoľného komplexného čísla vo forme p + qi. abs (2 + 3i) = druhá odmocnina (2 2 + 3 2) = (13) 0, 5
uhol: Nájsť fázový uhol komplexného čísla.

Existujú určité tipy, ktoré by sa mali dodržiavať v záujme správneho fungovania komplexných čísel v Matlabe, ako napríklad:

Mali by sme sa vyhnúť použitiu i a j ako súčasti akýchkoľvek premenných mien, pretože sa používajú na označenie imaginárnych častí komplexného čísla.
Mali by sme sa vyhnúť použitiu j alebo i, ak je imaginárna časť 1. Namiesto toho môžeme použiť 1j alebo 1i.
V Matlabe môžeme vytvoriť komplexnú funkciu, keď sa i a j používajú v niektorých častiach ako názvy premenných, vstupné argumenty nie sú jednoduchého ani dvojitého typu a imaginárna časť je nula.

záver

Komplexné čísla sa používajú v matematickej alebo inžinierskej oblasti. Pomocou imaginárnej časti zložitých čísel je možné opísať veľa aplikácií v reálnom alebo praktickom živote. Pochopenie používania a aplikácií zložitých čísel na rôznych platformách je preto dôležité najmä v prípade, že máte čo do činenia s fyzickou alebo matematickou doménou.

Odporúčané články

Toto je sprievodca komplexnými číslami v MATLABe. Tu diskutujeme o zavedení a komplexnom generovaní čísel v matlabe vrátane jeho príkladov s funkciou a funkciou. Viac informácií nájdete aj v nasledujúcich článkoch